Neden dünya denilen bu gezegendesin? Merak ediyorsan oku…
Evren hakkında her şey
Evren hakkında fikir jimnastiği
Evrenin, Euclides geometrisine uyup uymadığını bilmiyoruz. İnsan ölçeğinde uzayın eğriliği sıfırdır. Yani bir üçgenin iç açıları toplamı 180˚’dir. Bu durumda evren sonsuzdur. Fakat uzay eğri olabilir. Bugün biliyoruz ki büyük kütleler uzayı büker. Ayna etkisi sayesinde büyük kütleler arkalarında kalan gök cisimlerinin ayna görüntüsünü oluşturur. Yani uzayın eğri olmasının önünde bir engel yok. Kozmik ölçekte bu eğriliğin pozitif mi, negatif mi olduğu önemli olur. Eğer negatif ise evren Hiperboloid (semer şekilde) uzaydır. Öyle bir evrende üçgenin iç açıları toplamı 180˚’den azdır. Eğer evrenin eğriliği pozitif ise hiperküre evren olur. Böyle bir evrende üçgenin iç açıları toplamı 180˚’den fazladır.
Hiperküre evren kapalı bir hacme sahip olmasına karşılık hayalet imgeler yüzünden sonsuz algısı oluşturur. Böyle bir evrende gözlemci sınırlı sayıda galaksi olmasına rağmen sonsuz sayıda galaksi görür. Fakat sonlu olduğu için fizikçilerin ilgisini daha çok çeker. Çünkü fizikçiler sonsuzluktan hoşlanmazlar.
Sicim kuramı da ilginç bir şekilde bu durumu kullanır. Fakat önce sicim kuramının bize sunduğu önemli bilgileri Sayın Brean Greene’in kaleminden okuyalım.
Brean Greene’in kitabı Evrenin Zerafeti’nden derlenen Sicim Teorisine göre evrenin yapısı…
Sicim fiziğinin temelini bulabilmek için bahçe hortumu şeklinde bir evren tasviri yapılabilir. Biri uzamış diğeri kıvrılmış iki boyuttan oluşan bu evrende nokta parçacıklar; titreşim hareketi ile hortum çevresinde ve boyunca hareket edebilir. Benzer hareketleri sicimlerde yapabilir.
Biz nokta parçacıkların hareketiyle sicimlerin hareketi arasındaki bir farkla ilgileniyoruz; sicimin hareket ettiği uzayın şekline doğrudan bağlı bir farkla. Sicimin bir boyutu olduğundan, titreşim hareketi dışında başka bir olası hareket şekli daha söz konusudur: Şekil 1’de görüldüğü gibi sicim Bahçe Hortumu evrenin dairesel kısmına sarılabilir (deyim yerindeyse bir kement gibi).
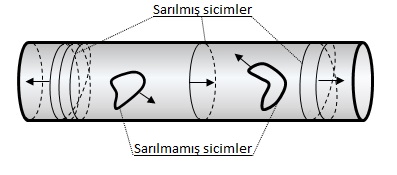
Şekil 1 Hortum evrene sarılmış ve sarılmamış sicimler
Sicim hortum üzerinde kaymaya ve salınmaya devam edecektir, fakat bunu yer kaplayarak yapacaktır. Aslına bakarsanız, sicim uzayın dairesel kısmını pek çok defa sarabilir. Hortum boyunca kayarken de yine salınım hareketi gerçekleştirecektir. Bir sicim böyle sarılmış bir şekildeyse eğer, sarmal halde olduğunu söyleriz. Belli ki sarmal hal, sicimlere özgü bir olasılıktır. Nokta parçacıklarda bunun karşılığı yoktur. Şimdi, bu niteliksel olarak yeni sicim hareketinin hem sicimin kendisi hem de sardığı boyutun geometrik özellikleri üzerindeki etkisini anlamaya çalışalım.
……..
Sicimlerin sarılmış halde de bulunabilme olasılığı, Bahçe Hortumu evrendeki bir sicimin enerjisinin iki kaynaktan geldiğini gösterir: Titreşimli hareket ve sarmalama enerjisi. Kaluza ile Klein’ın mirasına göre, bunların ikisi de hortumun geometrisine, yani hortumun kıvrılmış dairesel bileşeninin yarıçapına dayanmaktadır, fakat bu belirgin bir biçimde sicimlere özgüdür; çünkü nokta parçacıklar hortumun boyutlarını saramaz. O halde ilk işimiz sarmalama enerjisinin ve titreşimin, sicimin enerjisine katkısının dairesel boyutun büyüklüğüne tam olarak nasıl bağlı olduğunu belirlemek olacak. Bu amaçla, sicimlerin titreşim hareketlerini iki gruba ayırmak uygun: Birörnek ve sıradan titreşimler. Sıradan titreşimler, olağan salınımları ifade eder. Birörnek titreşimlerse daha da basit bir hareketi ifade eder: Sicimin şeklini değiştirmeden, bir yerden diğerine kayarken yaptığı hareket. Bütün sicim hareketleri kaymanın ve salınmanın -birörnek ve sıradan- titreşimlerin bir bileşimidir, fakat şimdi tartıştığımız konu açısından sicimlerin hareketlerini bu şekilde ayırmak işimizi kolaylaştıracaktır.
İşte iki temel gözlem. İlki, bir sicimin birörnek titreşimlerinin enerjisi, dairesel boyutun yarıçapıyla ters orantılıdır. Bu, kuantum mekaniğinin belirsizlik ilkesinin doğrudan bir sonucudur: Yarıçap küçülürse sicim daha katı bir biçimde sınırlanır, dolayısıyla -kuantum mekaniğine özgü “kapalı yer korkusu” yüzünden- hareketinin enerjisini artırır. Yani dairesel boyutun yarıçapı küçüldükçe, sicimin hareketinin enerjisi mutlaka artar; bu ters orantılı olmanın ayırt edici özelliğidir. İkincisi, sarmal hal enerjisi yarıçapla -ters değil- doğru orantılıdır. Bunun, sarılmış sicimlerin minimum uzunluğunun, dolayısıyla da minimum enerjilerinin yarıçapla doğru orantılı olduğu için böyle olduğunu unutmayın. Bu iki gözlem, yarıçapın büyük değerlere sahip olmasının sarmalama enerjilerinin büyük, titreşim enerjilerinin küçük olması, yarıçapın küçük değerlere sahip olmasının da sarmalama enerjilerinin küçük, titreşim enerjilerinin büyük olması anlamına geldiğini ortaya koyar.
Bütün bunlar da bizi, kilit olguya götürüyor: Bahçe Hortumu evrendeki her büyük dairesel yarıçapa karşılık gelen, büyük yarıçaplı evrendeki sicimlerin sarmalama enerjilerinin küçük yarıçaplı evrendeki sicimlerin titreşim enerjilerine, büyük yarıçaplı evrendeki sicimlerin titreşim enerjilerinin de küçük yarıçaplı evrendeki sicimlerin sarmalama enerjilerine eşit olduğu küçük bir dairesel yarıçap vardır. Fiziksel özellikler, bir sicimin şeklinin toplam enerjisine -bu enerjiye titreşimin ne kadar, sarmal hareketin ne kadar katkıda bulunduğuna değil- duyarlı olduğundan, Bahçe Hortumu evren için geometrik olarak farklı bu biçimler arasında hiçbir fiziksel fark yoktur. İşin tuhafı, sicim kuramı “dolgun” bir Bahçe Hortumu evrenle “ince” bir Bahçe Hortumu evren arasında hiçbir fark olmadığı iddiasındadır. Sayfa 284-289
…….
Bir sicim bir masanın ya da bahçe hortumunun yüzeyi gibi ikiboyutlu bir yüzey üzerinde uzanmakla sınırlanırsa, titreşebileceği bağımsız doğrultuların sayısı ikiye iner: Yüzey üzerinde sağ-sol ve ileri-geri boyutu. Yüzeyde kalan her titreşim örüntüsü, bu iki yöndeki titreşimlerin bir bileşimini içerir. Buna uygun olarak, bu söylediklerimizin Düzülke’de, Bahçe Hortumu evrende ya da ikiboyutlu başka bir evrende bir sicimin de toplamda iki bağımsız uzamsal doğrultuda titreşmekle sınırlı olduğu anlamına geleceğini görmekteyiz, aynı zamanda. Fakat bir sicimin yüzeyden ayrılmasına izin verilirse, bağımsız titreşim doğrultularının sayısı da üçe çıkacaktır, çünkü bu durumda sicim yukarı-aşağı doğrultusunda da salınabilecektir. Gözümüzde canlandırmak giderek zorlaşsa da bu örüntü uzayıp gitmektedir: Daha çok sayıda uzamsal boyutlar içeren bir evrende sicimin titreşebileceği bağımsız doğrultuların sayısı da o kadar fazladır.
Sicimlerin titreşimiyle ilgili bu olguyu özellikle vurguluyoruz, çünkü fizikçiler, sorun çıkaran hesapların bir sicimin titreşebileceği bağımsız doğrultuların sayısına son derece duyarlı olduğunu bulmuşlardı. Negatif olasılıklar, kuramın gerektirdiğiyle gerçekliğin dayatır göründüğü şey arasındaki bir uyumsuzluktan doğuyordu: Hesaplar, sicimler birbirinden bağımsız dokuz uzamsal doğrultuda titreşebilecek olsa, tüm negatif olasılıkların ortadan kalkacağını gösteriyordu. Kuram açısından iyi bir şeydir bu, fakat gerisi? Sicim kuramının dünyamızı uzamsal üç boyutla açıklaması bekleniyorsa, başımız hâlâ dertte demektir.
Ama, acaba böyle midir? Yarım yüzyıldan daha eski bir yolu izlediğimizde, Kaluza ile Klein’ın bir gedik açtığını görüyoruz.
Sicimler çok küçük olduklarından, yalnızca geniş, uzamış boyutlarda değil, ince ve kıvrılmış boyutlarda da titreşebilirler. Bu nedenle Kaluza ve Klein nın yaptığı gibi, bildik, uzamış üç uzamsal boyuta ek olarak diğer altı kıvrılmış uzamsal boyutun bulunduğunu varsayıp sicim kuramının evrenimizde dokuz uzay boyutunun varlığını gerektirdiğini kabul edebiliriz. Böylece, fizikte kayda değer konular arasındaki yerini kaybetme tehlikesiyle karşı karşıya görünen sicim kuramı bu tehlikeden kurtulmuş oluyor. Bunun da ötesinde, sicim kuramı Kaluza ile Klein ve onları takip edenlerin yaptıkları gibi fazladan boyutları varsaymaktan çok, bu boyutların varlığını gerektirmektedir.
Sicim kuramının anlamlı olabilmesi için, evrende dokuz tane uzay boyutu ve bir de zaman boyutuyla birlikte, toplam on boyut olması gerekir. Bu şekilde, Kaluza’nın 1919’daki önerisi en ikna edici ve güçlü savunmasını buluyor. Sayfa 244-245
……..
Tartışmamız Bahçe Hortumu evrende geçiyor olsa da basit olsun diye kendimizi biri uzamış biri de kıvrılmış iki uzamsal boyutla sınırlamıştık. Üç tane uzamış uzamsal boyutumuz, altı tane dairesel boyutumuz olsaydı da sonuç aynıdır. Dairelerin her birinin çapı, karşılığıyla değiştirildiğinde fiziksel olarak tamamen aynı evrenin oluşmasına yol açar.
Bu sonucu çok daha ileriye de götürebiliriz. Evrenimizde, gökbilimsel gözlemlere göre her biri 15 milyar ışık yılı uzunluğunda olan üç uzamsal boyut gözlüyoruz. Bu boyutlar sonsuza kadar devam mı ediyor, yoksa acaba teknoloji harikası teleskopların görsel duyarlılığının ötesinde, kendi üstlerine kıvrılıp devasa bir daire mi oluşturuyorlar bilmiyoruz, ikinci durum geçerliyse, uzayda seyahat eden bir astronot sürekli sabit bir doğrultuda giderse sonunda evrenin çevresini dolaşıp -tıpkı Macellan’ın Dünyanın çevresini dolaşması gibi- başlangıç noktasına geri dönecektir. Dolayısıyla bildiğimiz uzamış boyutlar da pekâlâ daire şeklinde olabilir ve yine dolayısıyla sicim kuramının Rpe 1/R fiziksel tanımlarına tabi olabilir. Kabaca rakamlarla konuşacak olursak, bildiğimiz boyutlar eğer daireselse, çapları yukarıda da belirttiğimiz gibi 15 milyar ışık yılı uzunluğunda olmalıdır; 15 milyar ışık yılı, Planck uzunluğunun 1061 katıdır, evren genişledikçe de büyümektedir. Sicim kuramı doğruysa, bu durum bildiğimiz boyutların yarıçaplarının yaklaşık 1/R=1/1061, yani Planck uzunluğunun 1061 gibi inanılmayacak kadar kısa bir uzunlukta olması halinde ortaya çıkacak dairesel evrenle fiziksel olarak tamamen aynıdır! Bunlar şu bildiğimiz boyutlar, ama şimdi onları sicim kuramının sunduğu alternatif bir tanım çerçevesinde görüyoruz.
Aslına bakarsanız bu karşılıklı dilde, bu küçük daireler zamanla giderek ufalacaktır, çünkü R büyürken 1/R küçülecektir. İşte şimdi gerçekten de her şey karıştı. Nasıl olur da böyle bir şey mümkün olabilir? Nasıl olur da 1,80 metre boyunda bir insan, böyle inanılmaz derecede mikro bir evrene “sığabilir”? Nasıl olur da zerre kadar bir evren, başımızı kaldırınca gördüğümüz o muazzam genişlikle fiziksel olarak tamamen aynı olabilir? Sayfa 297-298
Sicim Kuramında Birbirine Bağlı İki Mesafe Kavrayışı
Mesafe, dünyayı kavrayışımızda öyle temel bir kavramdır ki, ne kadar ince ayrıntılar barındırdığını gözden kaçırmak çok kolaydır.
Özel ve genel görelilik kuramlarının uzay ve zaman kavrayışlarımızda yol açtığı şaşırtıcı etkiler ve sicim kuramından doğan yeni özellikler, mesafeyi daha tanımlarken bile bizi dikkatli olmaya zorlar. Fizikteki en anlamlı tanımlar işlemsel tanımlardır, yani en azından prensipte, tanımlanan şeyi ölçmenin bir yolunu sunan tanımlar. Ne de olsa, bir kavram ne kadar soyut olursa olsun elimizde işlemsel bir tanımının olması, o kavramın anlamını, kavramın değerini ölçebileceğimiz deneysel bir sürece dönüştürmemizi mümkün kılar.
Mesafe kavramının işlemsel bir tanımını nasıl yapabiliriz? Sicim kuramı bağlamında bu sorunun cevabı bir hayli şaşırtıcıdır. 1988’de iki fizikçi, Brown Üniversitesi’nden Robert Branden-berger ile Ffarvard Üniversitesinden Cumrun Vafa, eğer bir boyutun uzamsal şekli daireselse, sicim kuramında birbirinden farklı ancak birbiriyle ilişkili, işlemsel iki mesafe tanımı olacağını göstermişti. Bu tanımların ikisi de, mesafenin ölçülmesi için farklı bir deneysel süreç ortaya koyar ve iki süreç de kabaca söyleyecek olursak, eğer bir “birim sicim” sabiti, bilinen bir hızda yol alıyorsa, “birim sicim”in o mesafeyi ne kadar zamanda kat ettiğini belirleyerek ölçebilecek olmamız gibi basit bir ilkeye dayanır. İki süreç arasındaki fark kullanılan “birim sicim”dedir. İlk tanımda dairesel bir boyuta sarılmamış sicimler, ikinci tanımdaysa dairesel bir boyuta sarılmış sicimler kullanılır. Görüyoruz ki, sicim kuramında mesafeye dair işlemsel iki doğal tanım olmasının gerisinde temel “birim sicim”in boyuta sahip olma özelliği vardır. Sarmalama kavramının olmadığı nokta parçacık kuramında, mesafenin tek bir işlemsel tanımı olacaktır. Sayfa 298-299
Bu iki sürecin sonuçları arasında nasıl bir fark vardır? Brandenberger ve Vafa’nın bulduğu cevap hemen anlaşılabilir olmadığı gibi şaşırtıcıdır da. Sonucun ardındaki ilk fikir, belirsizlik ilkesine başvurularak anlaşılabilir.
Sarılmamış sicimler serbestçe hareket ederek dairenin R ile doğru orantılı olan çevresini dolaşabilir. Belirsizlik ilkesine göre, sicimlerin enerjileri 1/R ile doğru orantılıdır. Öte yandan sarılmış sicimlerin minimum enerjisinin R’yle doğru orantılı olduğunu görmüştük; belirsizlik ilkesi bu sicimlerin “birim sicim” olarak R’nin karşılığına, yani l/R’ye duyarlı olduğunu söyler. Bu fikrin matematiksel olarak somutlaşması, eğer her ikisi de dairesel boyutun yarıçapını ölçmekte kullanılırsa, sarılmamış sicimlerin yarıçapı R olarak, sarılmış sicimlerin 1/R olarak ölçeceğini gösterir; mesafeleri Planck uzunluğunun katlarıyla ölçüyoruz.
İki deneyde de varılan sonuçlar aynı derecede geçerlilik iddiası taşımaktadır. Mesafe ölçmek için farklı “birim sicim”ler kullanıldığında farklı cevaplar alacağımızı sicim kuramından öğrenmiştik. Aslına bakarsanız bu özellik, yalnızca dairesel bir boyutun büyüklüğünün belirlenmesinde değil, bütün uzunluk ve mesafe ölçümleri için geçerlidir.
Sarılmış ve sarılmamış sicimlerden oluşan “birim sicim”lerle elde edilen sonuçlar birbirleriyle ters orantılı bir ilişki içinde olacaktır. Eğer sicim kuramı evrenimizi tanımlıyorsa, bu olası iki mesafe kavramıyla gündelik hayatta ya da bilimsel uğraşlarımızda neden hiç karşılaşmadık acaba? Ne zaman mesafeden bahsetsek, hep bir tek mesafe kavramının olduğu, ikinci bir mesafe kavramanın olması ihtimalinin bile olmadığı yönündeki deneyimimizle uyuşan bir tarzda konuşuyoruz. Alternatif olasılığı neden gözden kaçırmışız? Bu sorunun cevabı şu: Tartışmamızda yüksek derecede bir simetri olsa da, R’yi (dolayısıyla1/R’nin de) 1’den (yani Planck uzunluğunun 1 katı) önemli ölçüde farklı olması halinde, işlemsel tanımlarımızdan birini uygulamak son derece güçken, diğerini uygulamak son derece kolaydır. Esasında başka bir olasılık daha olduğundan tümüyle habersiz bir halde, daima kolay yaklaşımı uygulamışızdır.
İki yaklaşımın zorluk derecelerinin farklı olmasının nedeni, R yarıçapının (dolayısıyla 1/R’nin de) Planck uzunluğundan (yani R=1’den) çok farklı olması durumunda kullanılan “birim sicim”lerin (yüksek sarmalama enerjili/düşük titreşim enerjili ve tersi) kütlelerinin çok farklı olmasıdır. Planck uzunluğundan çok farklı yarıçaplar söz konusu olduğunda, “yüksek” enerji inanılmaz derecede büyük kütleli “birim sicim”lere (örneğin protondan milyar kere milyar kat daha ağır parçacıklara), “düşük” enerji ise sıfırdan en fazla bir zerre fazla bir kütlesi olan “birim sicim”lere karşılık gelir. Bu koşullarda, iki yaklaşımın zorluk derecesi arasındaki fark çok çok büyüktür, çünkü ağır sicim şekillerini üretmek bile bugünkü teknolojik yetilerimizin ötesindedir. O halde, iki yaklaşımdan yalnızca biri teknolojik olarak uygulanabilir: İki sicim şeklinden hafif olanın kullanıldığı yaklaşım. Bu yaklaşım, buraya kadar mesafeyle ilgili bütün tartışmalarımızda üzeri örtük olarak kullanılan yaklaşımdır. Bize bilgi veren ve sezgilerimizle uyuşan yaklaşım budur.
Uygulanabilirlikle ilgili konuları bir kenara bırakırsak, sicim kuramının yönlendirdiği bir evrende mesafeleri bu iki yaklaşımdan birini kullanarak ölçmekte serbestiz. Gökbilimciler “evrenin büyüklüğünü” ölçerken, bunu kozmosta dolaşan ve tesadüfen teleskoplarının menziline giren fotonları inceleyerek yapar. Bu durumda fotonlar sicimlerin hafif halleridir. Elde edilen sonuç, daha önce de bahsettiğimiz üzere Planck uzunluğunun 1061 katıdır. Bizim için tanıdık olan üç uzamsal boyut gerçekten daireselse ve sicim kuramı da doğruysa, son derece farklı (ve halihazırda var olmayan) cihazlar kullanan gökbilimcilerin, prensipte, evrenin genişliğini sarılmış haldeki ağır sicimlerle ölçebilmesi ve bu büyük mesafenin karşılığı olan bir sonuca varması gerekir, işte bu anlamda, evreni ya normalde yaptığımız gibi çok büyük ya da çok çok küçük olarak düşünebiliriz. Hafif sicim hallerine göre evren büyüktür ve genişlemektedir, ağır sicim hallerine göreyse küçüktür ve büzüşmektedir. Burada bir çelişki yoktur, aksine elimizde birbirinden tamamen farklı, fakat aynı derecede anlamlı iki mesafe tanımı var. Teknolojik sınırlılıklar yüzünden ilk tanımı çok daha iyi biliyoruz, ama yine de iki tanım da aynı derecede geçerli kavramlardır. Sayfa 284-301
Sayın Brean Greene’in Evrenin Zerafeti adlı kitabından derlediğim bu satırlardan anlamamız gereken en önemli şey evrenin büyüklüğünün izafi olduğudur. İki uzaklık kavramı çok anlaşılır olmadığı için şöyle örnekleyelim. 1 m’lik bir parkurda fil ile karıncayı yarıştırmaya benzer bir durum var. Fil başlangıç çizgisine arka ayaklarını koyduğunda ön ayakları bitiş çizgisinin hayli önünde olur. Oysa karınca için bitiş çizgisine muazzam bir yol var demektir. İşte bizim “birim sicim” olarak fil ile karıncayı almamıza benzer bir durum var ortada. Eğer “birim sicim” olarak hafif sicimi alırsak evren muazzam büyüklükte bir yerdir. Fakat “birim sicim” olarak ağır sicimi aldığımızda evren Planck büyüklüğünden muazzam derecede küçük demektir. Peki evren gerçekte hangisidir. Bu soruyu cevaplayabilmek için fil karınca örneğinden gidersek 1 m’lik yol olarak ortada bir parkur var. O parkura, karıncanın çok uzun ya da filin çok kısa demesi gibi bir şey. Parkur her ikisini de umursamaz. Evrende bizim tanımlamamızı umursamaz. O orada durmaktadır. Fakat bizim evreni tanımlamamız için “birim sicim” olarak hafif sicimi almamız, bize kolaylık sağlar.
Ayrıca yazıdan da anlayacağınız gibi bu büyüklükler boyutların çokluğu ya da açık veya kapalı olmalarıyla da ilgili değildir. Bizim üç boyutun açık ve diğer altı boyutun kapalı olduğu düşüncesi de pek geçerli değil. Açık boyut diye kabul ettiğimiz evren ağır sicim baz alındığında kapalı olduğu görülebilmektedir. Yani evrende üç uzay boyutu haricindekileri görmüyor oluşumuzun sebebi başka olmalı. Çünkü zaten ağır sicim haline göre bu üç boyutta kıvrık olmalıydı. Fakat bizim üç boyut için hafif sicimi kullanabiliyorken diğer boyutlar için kullanamıyor oluşumuzun bir başka sebebi olmalı. Daha sonra bu konuya tekrar değineceğiz.
Sayın Greene’in bu anlatımı bize evrenin yapısı konusunda muazzam açılımlar yapmıştır. Fakat bu sistemin kötü yanı konuya Sicim Kuramının temel oluşturmasıdır. Çünkü Sicim Kuramı henüz kesin olarak kabul edilmiş değildir. Bunun sebebi matematiğinin mükemmel olmasına rağmen, deneysel bir veriye henüz ulaşılmamış olmasıdır. Fakat bizim oluşturacağımız teori sicim kuramının esasları üzerine kurulu olduğu için onu doğru kabul edip ona göre devam edeceğiz.
Evrenin yapısını anlamaya devam etmeden önce, bazı konuları belirtmem gerekir. Örneğin; oluşturacağımız teori var olan diğer teorileri de içeren bir yapıda olacaktır. Yani, bu teori standart model teorisi gibi pek çok diğer teorileri de içeren bir yapıda olacaktır. Pek çok teorinin genel yapıda bir yeri tariflediğini ama, durumun körlerin bir fili tanımlaması gibi, her teori diğeriyle bağ kuramadığı için ayrı kaldığını anlayacağız.
Bilim, parçacık hızlandırıcılarda bulduğu parçacıkların farklı boyutlara ait parçacıklar olduğunu düşünmez. Fakat biz bir atomun yapı taşları olarak Proton, Nötron ve Elektronu biliriz. Her atom, bu elemanların çeşitli versiyonları şeklinde karşımıza çıkar. Oysa biz atomu 3 boyutlu eleman olarak alıp parçaladığımızda oluşan parçacıkların, bir üst boyutun elemanları olduğunu düşünmeliyiz. Aslında boyut dediğimiz şey maddenin içinde saklı. Bilimin bunu düşünmemesinin sebebi bu elemanları kolaylıkla elde etmesidir. “Kolaylıkla elde edilebiliyorlarsa, içinde bulunduğumuz boyutun elemanlarıdırlar” diye düşünür. Fakat bize en yakın boyut ile o kadar yakınız ki zaten tek boyut gibi algılamış olmamız normaldir. Oysa protonların parçalanmasıyla elde edilen kuarklar, aynı durumda değil. Çünkü onlar bizden 2 boyut ötededirler. Onun için serbestçe elde edemeyiz.
Üç boyutlu atomu parçaladığımızda elde ettiğimiz parçacıklar dört boyutlu uzayın bir elemanıysa durum daha anlaşılır olur. Ya da 4 boyutlu protonu parçaladığımızda 5 boyutlu kuark elde ettiğimizde daha da netleşir. Elbette parçacıkların hangi boyuta ait olduklarını gösteren bir argümanımız yok. Çünkü, o parçacıkları biz noktasal görmekteyiz. Yani kütleleri var, büyüklükleri var ama kapladıkları yer noktasaldır. Aslında noktasal da değiller. Tamamen dalgadan oluşurlar. Teorimizde bu dalganın oldukça önemli yeri olacak. Bahsettiğim dalganın şöyle bir özelliği var. Dalga hızı belli bir seviyenin altındaysa gözümüze ve alıcılarımıza yakalanır, değilse yakalanmaz.

Şekil 2 Kuantum evren ile görünen evrenin yapısı
Bizim parçacık hızlandırıcılarda elde edeceğimiz her parçacık, enerji seviyesi olarak en düşük düzeyden alındığı için, bizi biraz yanılttığını anlamalıyız. Durumu daha iyi anlayabilmek için şekil 5’i incelemeliyiz. Şekildeki en dıştaki kabuk, atomu temsil eder. Atom parçalandığında alt parçacıklar bir üst boyutun elemanları olarak, o uzayın serbestçe var olabilen elemanları olur. Oysa o parçacıkları kolaylıkla elde ediyor olmamıza rağmen, 3 boyutlu uzayın serbest elemanları değildirler. Üç boyutun serbest elemanları atomlardır. Atomlar bile doğada pek serbestçe bulunmaz. Genellikle başka atomlarla bağ oluştururlar.
Eğer bir atom parçalanırsa, 4 boyutlu ortamda serbestçe olabilecek elemanların bulunduğu bir uzaya geçmiş demektir. Fakat burada da şöyle bir durum var. Atom, tüm kuantum katlarının en altındadır. Oluştuğu elemanlarda yine aynı dalga frekansına inmiştir. Proton ve nötron olarak yine atomun bulunduğu en alt düzeyde var olabilirler ama eğer kuarka geçersek, bu sefer atomun bulunduğu yerde bulunamazlar. Frekans ve enerji seviyeleri buna izin vermez. Ancak birleşip proton ya da nötron oluşturduklarında, o seviyeye inebilirler. Çünkü, birleştikleri zaman dalga frekansları azalarak enerji seviyelerini düşürürler. Bu durum evrenin oluşum mekanizmasıdır. Yani, frekansı yüksek parçacıklar birleşerek kütle olarak büyük parçacık oluşturduklarında, hem enerjileri hem de frekansları düşer. Bu konuya ilerde tekrar değineceğiz ama, şimdilik anlamamız gereken şey, içinde bulunduğumuz üç boyutun, tüm evren içinde çok küçük bir bölümü oluşturduğudur.
Boyutlar arası enerji farkları var. Fakat biz bir atomu parçalarken kullandığımız enerji çok az olmasına rağmen yukarı çıkıldıkça, bu miktar artar. Onun için bir atomun bozunmasına zayıf kuvvet yetebilirken daha yukarısı için muazzam enerji gerekir. Çünkü, protonu elde edebilmek için atom çekirdeğini ancak dört temel kuvvetten biri sayılan güçlü kuvveti uygulayarak parçalayabiliriz. Fakat ilerde anlayacağımız gibi bu kuvvetler çok daha fazladır. Ve bu kuvvetlerin en zayıfı, güçlü nükleer kuvvettir.
Dediğimiz gibi gördüğümüz evren, büyük evren fotoğrafında çok küçük bir yer tutar. Onun için anlam karmaşası olmaması açısından evren tanımımızı netleştirmemiz lazım. Çünkü bu kuramda görebildiğimiz evren yanında, göremediğimiz evrenlerde var. Onun için gözle ya da optik aletlerle görebildiğimiz evrene “Görünen evren” adını vereceğiz. Şekil 2’de en altta olan düzeye karşılık gelir. Şekilde astral düzey ile 11 boyutlu evren arasında kalan yere ise kuantum evren ve her kata da kuantum katı diyeceğiz. Katları ise boyut sayısıyla anacağız. Bu durumu 11 boyutlu uzay içinde, 10 boyutlu bir kabarcık gibi düşünürsek daha kolay anlarız. Kuantum evreni görmüyoruz ama parçacık hızlandırıcılarla bize en yakın parçacıklarını bulabiliyoruz. Hatta, kuantum evrene ait bazı maddeleri göremediğimiz halde, kütle çekim etkisini tespit edebiliyoruz. Yani görünen evrenimiz kuantum evrenden oldukça etkilenmekte ve orayı etkilemektedir. Kuantum evrenin zaman ve mekân yönünden durumu şöyledir.
- Görünen evren, 3 mekân 1 zaman boyutlu,
- Birinci kuantum katı, 4 mekân 1 zaman boyutlu,
- İkinci kuantum katı, 5 mekân 1 zaman boyutlu,
- Üçüncü kuantum katı, 6 mekân 1 zaman boyutlu,
- Dördüncü kuantum katı, 7 mekân 1 zaman boyutlu,
- Beşinci kuantum katı, 8 mekân 1 zaman boyutlu,
- Altıncı Kuantum katı, 9 mekân 1 zaman boyutlu,
- Yedinci kuantum katı, 10 mekân 1 zaman boyutlu.
Çizeceğimiz şekillerde kuantum evreni oluştururken 1 zaman boyutunu göstermeyeceğiz ama var olduğunu bileceğiz. Ayrıca ilerde yeri geldikçe evren tanımımızı genişleteceğiz. Çünkü evren çok daha kapsamlı bir yapıdır. Sicim Kuramı 10 boyutlu bir evren önerir ama M kuramı 11 boyutlu bir evren önerir. Benim önerim ise 11 mekân ve 1 zaman boyutlu bir yapıdır. Yani içinde bulunduğumuz 10+1 boyutlu evren 11 mekân boyutlu bir yer içinde 10 mekân ve 1 zaman boyutlu bir kabarcık şeklinde olacaktır. Bu 11 mekân boyutlu yer içinde bizim evrenimize benzer pek çok evren olmuş olabilir. Fakat oranın yapısı hakkında çok az bilgimiz vardır. Zaten biz bu yer ile değil, içinde oluşan 10+1 boyutlu kabarcık evren ile ilgileneceğiz.
Buraya kadar anlatmaya çalıştığımız evrenin yapısını, şekil 2’den takip ederek anlamaya çalışalım. O şekil, hatta kullanacağımız hemen her şekil maddenin dalga frekansını baz alarak oluşturulmuştur. Bu frekanstan, sicimlerin titreşimi olarak zaten daha önce bahsetmiştik. En altta olan “GÖRÜNEN EVREN” diye tasvir edilen yer, kuantum evren dışında ama ona bağlı, gözle veya optik aletlerle gördüğümüz her şeyi kapsar. Yani açık olan üç boyutun olduğu yer. Aslında astral düzey ile görünen evren aynı yerdedir ama aralarında biraz nüans farkları var. Örneğin biz görünen evren için hafif sicimi “birim sicim” olarak düşünürken astral düzey ve yukarısı için ağır sicimi düşünerek değerlendireceğiz. Çünkü hafif sicim bize görünen evren için kolaylık sağlarken ağır sicim, kuantum evren için kolaylık sağlar. Onun için o noktayı ayırmamız gerekir. Her iki bölüm pek çok ortak denklemle temsil edilmesi yanında kuantum evrende hız ve mesafe kavramı görünen evrende olduğu gibi olmadığı herkes tarafından bilinen bir durumdur.
Şekil 2’de tanımlanmış frekanslar gerçek değerler değildir. Fikir vermesi açısından ışığın frekansları düşünülerek oluşturulmuştur. Gerçek değerlerin hesaplanması gerekir.
Aslında görünen evren içinde her maddeyi de göremiyoruz. Bunun sebebi, biz belli bir seviyeye kadar olan dalga frekansını görüyor olmamızdır. Dalga frekansı yüksek olan madde görüş alanımızdan çıkar ama onun kütle çekim etkisini hissetmeye devam ederiz.
Görünen evren tüm girdilerini “ASTRAL DÜZEY” diye tanımladığımız yerden alır demiştik. Evrende olan atomların tümü astral düzeydedir. Bizim evrende görebildiğimiz her şey, o düzeyin bize yansımasıdır. Yani o düzeyi, ışığın beynimizdeki yorumlanışı şeklinde gördüğümüz için görüntüyü bir yansıma olarak almaktayım. Sonuç olarak biz her şeyi beynimizin yorumlayabildiği şekliyle görebiliyoruz. Bunun salt gerçeği oluşturduğunu düşünmemiz doğru değil. Çünkü hatırlıyorsanız “madde aslında bir olasılık dalgasıdır” demiştik. Olasılık dalgası katı değildir. Fakat aynı olasılık dalgasına biz baktığımızda onu parçacığa çökertiyoruz.[2] İşte gördüğümüz şey tam gerçeği oluşturmadığını bundan dolayı söylüyorum. İnsan olaya dâhil olduğunda, madde dalga olmaktan vaz geçip parçacığa dönüşmekte. Bu yapı sadece görünen evren için geçerlidir. Çünkü görünen madde dışındaki maddeye bakamadığımız için onu çökertemeyiz.
Karanlık madde diye tanımladığımız göremediğimiz maddelerin görülememelerinin sebebi dalga frekanslarının belli bir değerin üzerinde olduğundan demiştik. Bu değeri şimdilik bilemiyoruz ama bu konu üzerinde çalışacak olanlar çok kolaylıkla tespit edip karanlık maddeyi görebilecek bir cihaz üretebilirler.
Yanlış anlaşılmaması için şunu belirtmeliyim ki proton gibi bir parçacığın dalga frekansı seviyesi astral düzeyi seviyesinde olabilir ve zaten atom içindekilerin hepsi öyledir. Bizim onu göremememiz için bağımsız olarak dalga frekansının artması gerekir. Daha önce, kuarkların dalga frekansının astral seviyesine inemeyeceğini söylemiştik. Bu da onun serbestçe elde edilemeyeceğini gösterir.
Dalga frekansının değişimini dönen bir kütlenin hareketiyle özdeşleştirip ne demek istediğimi daha iyi anlatabilirim. Döner sandalyede kendi etrafında dönen birinin kucağına bir ağırlık koyduğumuzda hızının yavaşladığını görürüz. İki parçacık da ayrı ayrı dalga frekansları hızı, birleştiklerindeki ortak hızlarından fazladır. Yani birleşip toplam kütle arttığı için dalga frekansı azalır. Yeni parçacığın kütle olarak miktarı, iki parçacığın toplamı olmasına rağmen frekansı düşük olduğundan enerjisi de azalır. Bunu sağlayan şey Einstein’ın meşhur formülü E=mc2 formülüdür. Burada c görünen evrende ışık hızıdır ama kuantum evrenlerde dalga frekansına dönüşür. Görünen evren için sabit olan bu durum artık boyut yükselttikçe artan bir yapıya dönüşür. Kütle artış ya da azalışı parçacığın enerjisine frekansı kadar etki etmez. Çünkü frekans hem büyük bir rakamdır hem de karesiyle etki eder.
Büyük Patlama ve sonrası
Büyük Patlama ve sonrası diyorum ama Büyük Patlamanın az öncesinden başlamak zorundayız. Çünkü evrenin oluşumu, menbranların çarpışmasından başlar. Bu durumu şöyle senaryolaştıralım.
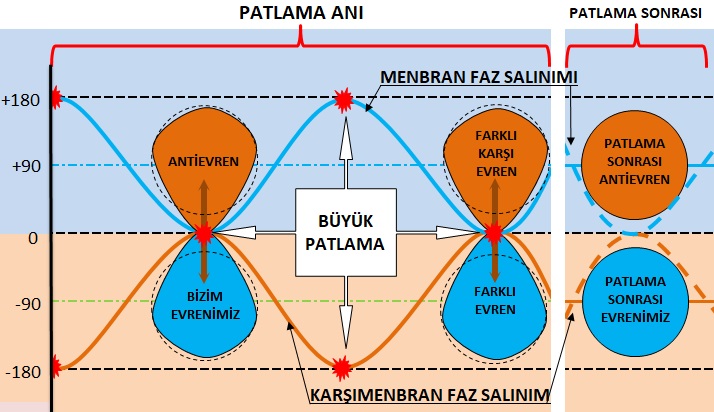
Şekil 3 11 boyutta oluşan patlama ve sonraki durum.
Evreni, 11 mekân boyutlu bir uzayda bulunan iki menbranın salınımının tepe noktalarında çarpışması sonucu oluşan, 10+1 boyutlu kabarcık olarak düşünelim. Şekil 3’de mavi ve kırmızı renkte ki yerler, +90 derece ile -90 derecedeki menbranların bölgesidir. Menbranların kendi bölgelerinde, birer sinüs dalgası şeklinde ve zıt yönlü salınmaları sonucu, tepe noktalarının birbirini algılamaları durumunda oluşan patlamaların her birine “Büyük Patlama” diyeceğiz. Bu patlamalar sürüp giderken biz sadece bir patlamayla ilgileneceğiz. Ters yönlü salınan menbranların ikisi de sıfır derece (veya +180 derece ile -180 derece) fazına ulaştığında, birbirini algılamasına çarpışma diyoruz. Çarpışmada oluşan şeyleri isimlendireceğiz ama şimdilik şarapnel diyelim. Çarpışma sonrası oluşan şarapneller dağılır ve enerji kaybederler. Kaybettikleri enerji yüzünden içinde bulundukları 11 boyutlu uzayda kalamayacak seviyeye düşerler. Böylece 10 boyutlu bir kabarcık oluşturup şarapnellerin dağılma sürecini de kapsayan bir süreç başlar.
Menbranların özelliklerini pek bilmiyoruz ama, oluşan patlamanın nasıl bir şey olduğu hakkında yorum yapabiliriz. Bir madde ile anti maddenin birleşmesinde ne oluşuyorsa, bu menbranların çarpışmasında tam tersi oluşur. (Çünkü bir madde ve antimadde birleştiğinde tekrar eski duruma dönüşmesi) Yani maddenin yok oluşunun tersi bir durum yaşanmış olması gerekir. Onun için menbranlardan birine anti menbran diyeceğiz. Bizi ilgilendiren asıl şey, oluşan kabarcığın içinde neler olduğudur. İlk olarak madde ve anti madde oluştuğunu düşüneceğiz ama, o seviyede oluşan maddelerin isimlerini sicim kuramından bildiğimiz için onları sicim ve anti sicim olarak adlandıracağız. 10 boyutlu uzayda kendilerini bulan sicim ve anti sicimler, hemen kendi karşı parçacıklarını bularak bildiğimiz Büyük Patlamayı oluşturur. Fakat aynı zamanda sıfır derece fazında olan sicimleri +90 derece ve -90 derece fazında olan menbranlardan biri çekerken diğeri iter. Aynı materyalden yapılı olanlar birbirini iterken, karşı olanlar çeker. Bu durum, aynı yüklü parçacıkların birbirini itmesi, karşı yüklü olanların çekmesi gibi bir durumdur. Sicimlerin bazısı antilerini bulup patlarken, bazısı antisini bulamadan, menbranlar tarafından çekilip kendi fazına sabitlenir. Anti sicimler Menbran, sicimler ise Anti menbran tarafından çekilerek birbirinden ayrılır. Sicimler +90 derece ve -90 derece fazlarında esir alınır. Tek kabarcık iki kabarcığa dönüşür. O sicimler, 10 boyutlu uzaya indiklerinden menbranla birbirlerine temas edemezler. Tıpkı karanlık maddenin kütle çekiminden etkilendiğimiz halde, ona temas edemiyor oluşumuz gibi. Artık sicimler kendi kaderlerini yaşamak zorundadırlar. Bu esnada, anti menbranın sicimleri çekmesi olayına “kütle çekim” diyeceğiz ve bu çekim tıpkı manyetik alan gibi, kendi alanını oluşturur. Eğer bu teori doğru ise, evrenimizde neden antimadde bulamayacağımızı da anlamış olduk. Sadece anlamadık onu bulabilmek için nereye bakmamız gerektiğini de, artık biliyoruz. Sicimlerin kaderini izlemeden önce, Büyük Patlama ve kütle çekim konusunu incelemeye devam edelim.
Kütle çekim tek kutuplu mudur?
“10 boyutlu uzayda oluşan sicimlerin bir kısmı birbiriyle birleşip yok olurken, bazısı buluşamadan ayrıldı” demiştik. İşte birbirinden ayrılan bu sicimler 10 boyutlu uzaya inmiş olmalarına rağmen, 11 boyutlu uzaydaki menbranlar tarafından çekilmeye devam ederler. Çünkü bu çekim, tüm boyutları aşan bir yapıdır. Kütle çekim dalgaları maddenin içinden boyutları aşar ve dışından ise, uzayı oluşturan dalgaları oluşturur. Onun için tek kutuplu gözükür. Çünkü kutbun öteki ucuna gidebilmek için, maddenin içinden yolculuk yapmak gerekir. Bizim “iki madde birbirini çekiyor” gibi görmemiz bu yüzdendir. Güneşin atomları içinden gelen anti menbranın çekim gücü Merkür’deki atomları çeker. Aynı şey Merkür için de geçerlidir. Böylece kütle çekimi tek kutuplu görürüz.
Boyutları aşan yapı yüzünden sicimler, anti menbranda; anti sicimler ise menbranda kilitli kalır demiştik. Sicimlerle menbranların birbirini çekmesi bir alan sayesinde olur. Bu alan tıpkı manyetik alan gibi çift kutupludur. Bir kutup atomken, diğer kutup menbrandır. İşte oluşan bu alan aynı zamanda bizim içinde bulunduğumuz uzayı oluşturur. Yani boşluk diye tanımladığımız şey, kütle çekim alanın kendisidir. Elbette manyetik alan gibi çizgilerden oluşur ama onlardan başka bir şey olmadığı için onu sürekli olarak görürüz. Oysa manyetik alan kütle çekim alanı içinde oluştuğu için çizgileri arasında boşluklar olabiliyor. Kütle çekimin oluştuğu bölgeye “hiçlik” diyebiliriz. Hiçlik içinden bir uzay alanı oluşmuş olur. Onun için uzayın dışında bir şey aramak saçmalıktır. Uzayın dışı olamaz. Aslında biraz önce 11 mekân boyutlu bir yerdeki menbranların çarpışması sonucu oluştuğumuzu söylemiştik. Tezat gibi görünen bu durumun bir açıklaması var. Onu evrenin yapısını tam olarak anladıktan sonra çözebileceğiz.
Evrende iki maddenin birbirini çekmesini kütle çekime bağlıyoruz. İki maddenin yakın mesafede birbirini ittiğini de biliyoruz. Yani, bir bardağı iki parmağımızın arasında tutmamız, bu kısa mesafeli itme kuvveti sayesinde olmaktadır. Böylece kütle çekimin etkisini yenerek bardağın yere düşmesini engelleyebilmekteyiz. Fakat bu durumun bir paradoks oluşturduğunu kimse düşünmez. Öyle ya! iki madde birbirini hem itip hem de çekmez. Bu mantıklı değil. Bu iki kuvvetin kaynağı aynı şey olamaz.
Evren ilk dönemde ışıktan hızlı genişlemiş olabilir mi?
Kütle çekim alanının oluşumu, maddenin oluşumu sırasında “aniden” olacaktır. Yani, oluşan sicimlerin miktarına bağlı olarak belli bir büyüklükte alan birdenbire oluşacaktır. Alan, hiçlik içinde oluştuğu için; ışık hızı sınırına tabi değildir. Işık hızı sınırı, kütle çekim alanı içindeki bir sınırdır. İşte bu şişme, Büyük Patlama anındaki ikinci şişmeyi sağlamış olacaktır. Bu şişme ışıktan hızlı olmasına rağmen, ışık hızı sınırını ihlâl etmiş olmaz.
Madde, sicimlerin çeşitli frekanslardaki görüntüsü mü?
Sicimlerin oluşumunu anlatmıştık. Büyük Patlama sonrası evrende bulunan sicimlerin frekansları azalmıştır. Haliyle sicimin sadece frekansı azalmaz, ona bağlı olarak enerjisi de azalır. Oysa 10 boyutlu uzay ancak belli enerji aralığındaki parçacıkları taşıyabilir. Sicimler kritik noktaya geldiğinde artık, 10 boyutlu uzayda kalamazlar. 9 boyutlu uzaya inmek zorunda kalırlar. Bunu yaparken, belli bir kütleye sahip sicimin, kütlesini koruyarak inebileceği enerji seviyesi sınırlıdır. O sınırın altına inildiğinde, sicimler birleşerek daha büyük bir kütle oluşturup, daha düşük frekansa sahip olarak, yeni uzaylarında yaşamağa devam ederler. İşte bu yeni parçacığa “9 parçacığı” diyeceğiz. Bilinmeyen parçacıkları boyut sayısıyla anacağız. 9 parçacığı da soğumaya devam ettiği için aynı şekilde enerji kaybetmeye devam edecektir. Böylece süreç atoma kadar bu şekilde oluşur. Elbette her boyutun çok çeşitli kararlı ve kararsız parçacıkları olacaktır. Bunlardan uygun olanlar, çeşitli sayı ve şekillerde birleşerek, yeni parçacıklara evrilecektir. Bu durum, evrenin doğal akış yönüdür. Haliyle evrendeki her maddenin frekansı, birleşen sicimlerin kütlesine karşılık gelen frekansa inmek durumundadır.
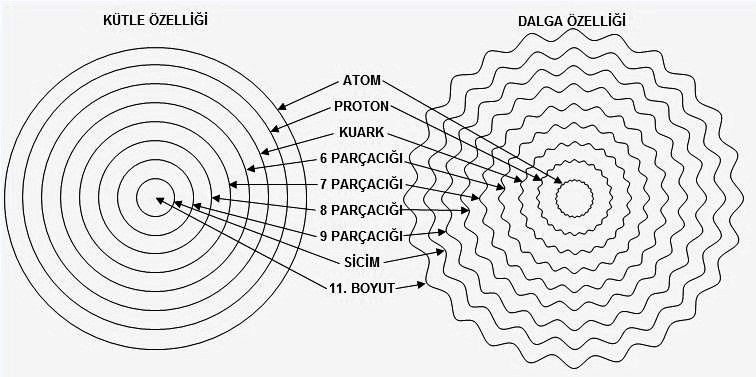
Şekil 4 Büyük daire, büyük kütle veya büyük dalga özelliği demektir.
Farkındaysanız bir boyuttaki parçacıkların oluşumu için, üst boyuttaki parçacıkların birleşmesi gerektiğini anlattık. Bu demektir ki tersi de mümkündür. Yani bir parçacığı bir şekilde parçaladığımızda bir üst boyuta ait elemanları elde etmiş oluruz. Bu durumda bir atomu parçaladığımızda elde ettiğimiz parçacıklar bir üst boyutun elemanları olmuş olur. Atom 3 boyutlu eleman ise; proton, nötron veya elektron 4 boyutlu uzayın elemanlarıdır. Kuark ise protonlardan elde edildiği için, 5 boyutlu uzayın elemanı demektir. Görüldüğü gibi atomdan sicime giden parçacıklar dizisi olmak durumundadır. Bu sıralama şekil 2, 4, 5 ve 6’da gözükmektedir.
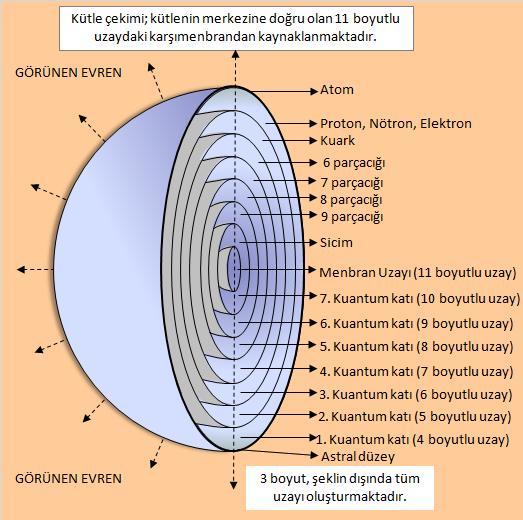
Şekil 5 Kütle çekim, 11. Boyuttaki menbranlardan kaynaklanır.
Boyutsal yapıyı anlayabilmek için, Şekil 5’i iyi anlamak gerekir. Orada görüldüğü gibi, bir üst boyut, maddenin iç yapısında gizlidir. En dıştaki kabuğu “atom” olarak düşünürsek; kabuğun kendisi ve dışı 3 boyutlu, içinde kalan alan ise, 4’ten 11 boyuta kadar olan katların, tümünü içerir. Atomun kabuğu parçalanırsa, 4 boyutlu uzay, dış uzay olur. O ortamdaki biri, hafif sicimleri baz alarak evrenin çok çok büyük olduğunu iddia edebilecektir. Eğer parçacık dış uzaya bakmıyorsa, onun için ağır sicim anlamlıdır. Hafif sicim sadece dış kabuk dışındaki parçacıklar için anlamlı olacaktır. Bizim için, en dıştaki kabuk atom olduğu için, görünen evren, atom ve onun bileşiklerinden oluşacaktır. Onun için, hafif sicim üç mekân boyutu için anlamlı sonuç verecektir. Diyelim ki! kuarkların hâkim olduğu bir evrende yaşasaydık, 5 mekân boyutlu uzayda olacaktık ve bu beş boyut için, hafif sicim anlamlı sonuçlar verecekti. O zaman 5 boyutun açık diğerlerinin kapalı olduğunu söyleyecektik.
Standart model ile sicim teorisinin neden birleşmediğini şekil 4’ten görebiliriz. Şekilde parçacıkların kütle ve dalga özellikleri görülmektedir. Kütlesi büyük olan parçacığın dalga frekansı küçüktür. Atom en ağır ama en küçük dalga frekansına sahip parçacıktır. Sicim ise kütle olarak en hafif ve en yüksek dalga frekansına sahip parçacıktır. Diğerleri aralara dağılır. Şekil 6’daki yapı bu parçacıkların genel durumlarını gösterir. Her boyut arasında bir kuvvet vardır. Bilimin bildiği 4 temel kuvvet içinde, sadece güçlü kuvvet bu tabloda yer alabilir. Çünkü güçlü kuvvet atom çekirdeklerinin parçalanarak, protonların elde edilmesini sağlar. Zayıf kuvvet atomların bozulmasını sağlar ama, boyutlar arası bir kuvvet değildir. Tam liste şekildeki gibidir. Şekil 6 gerçeğe yakın bir dizilim içerir ama, “kaç sicimden bir 9 parçacığı elde edebiliriz?” sorusunun cevabı şimdilik yoktur. Şekildeki miktarlar hayalidir ama bize kaba bir fikir verir. Şekilde belirtilenlerden sadece güçlü kuvvet ve renk kuvvetini biliyoruz. Gerçi renk kuvvetini bu şekilde tanımlamadılar, hatta onu temel kuvvet olarak bile düşünmüyorlar. Çünkü onu dört temel kuvvetin içine katıp beş temel kuvvet demiyorlar. Fakat, protondan kuark elde ederken aşılması gereken neyse biz ona renk kuvveti diyeceğiz.
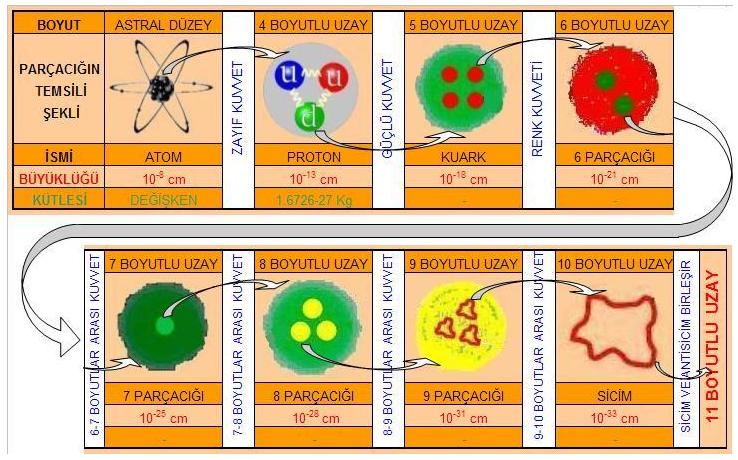
Şekil 6 Atomdan sicime parçacıklar listesi
Evren kütle kaybediyor olabilir mi?
Daha önce evrenin oluşum mekanizmasının, yani doğal sürecin, sicimden atoma doğru olduğunu söylemiştik. Acaba tersi durum söz konusu mudur? Yani evrende atomdan sicime doğru süreç var mı? Varsa bile bu sürecin doğal olamayacağı kesindir. Çünkü iki yöne doğal süreç olamaz. Yalnız evrendeki bazı göstergeler bunun da gerçekleştiği yönünde. Örneğin karanlık madde ve karanlık enerji bu yönün varlığına ciddi birer işaret.
Elbette evrenin kütle kaybetmesi, onun küçülmesi anlamına gelmesi gerekirken, tersi olması, durumu açmaza götürüyor gibi gözükmesine rağmen, durum aslında anlaşılabilirdir. Bu durumu anlayabilmek için, yine sicim kuramına dönüp “birim sicim” kavramına bakmalıyız. “Birim sicim” olarak, ağır sicimi alırsak, evren gittikçe küçülmektedir, oysa hafif sicim olarak alırsak, evren genişlemektedir. Evren, bizim neyi baz aldığımızla ilgilenmediğine göre, her iki durumda da gerçeğe ulaşmış olmamız gerekir. Oysa birini baz alınca genişliyor, diğerinde büzüşüyor olarak gözüküyor. Bu bir çıkmaz gibi görünse de her iki durumu da açıklayabilecek bir teori var. Eğer “evren kütle kaybediyorsa” her iki durumda mantıkla açıklanabilir.
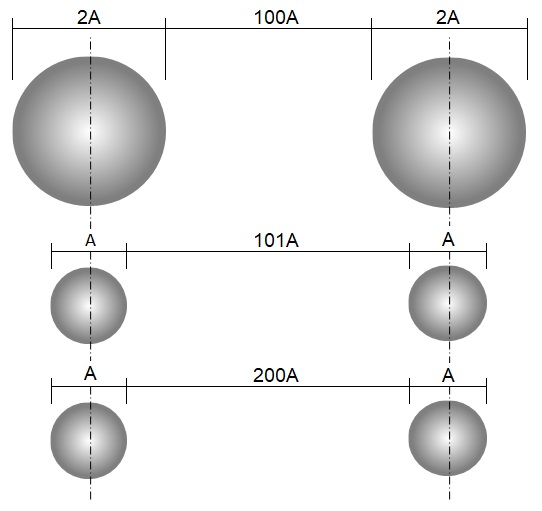
Şekil 7 Cisimler küçüldükçe aralarındaki uzaklık değişir.
Evren kütle kaybediyorsa, evrenin büzüşmesi gayet anlamlı olacaktır. Yani beklenen sonuçtur. Onun için “birim sicim” olarak ağır sicimin alınmasında bir sorun gözükmez.
Sorun, evren genişliyorsa vardır. Çünkü, evren kütle kaybettiği için, kütle çekim azalıyor, böylece Büyük Patlamada oluşan kaçış hızı gittikçe artıyor. Zaten evrende gözlenen durum, tamda budur. Yani bu durum “birim sicim” olarak hafif sicimi aldığımız durumla tam olarak örtüşüyor, gözükür. Oysa evren hem genişleyip hem büzüşemez.
Onu da şöyle açıklayabiliriz: yine “birim sicim” konusunu açarak durumu anlamaya çalışalım. Şekil 7’deki gibi iki tane 2A çapında cismimiz var. Eğer bu cisimlerin konumlarına dokunmadan çaplarını yarı yarıya küçültürsek aralarındaki mesafe 101A olur. Cisimlerden birinde bir gözlemci olduğunu düşünelim. Gözlemcinin “birim sicim”i cismin büyüklüğü olsun. Cisim, büyük haldeyken diğer cisimle aralarındaki mesafeyi 100A olarak ölçecektir. Yani iki cisim arasına 100 tane 2A boyutunda cisim sığacaktır. Oysa cisim küçüldüğünde onunda “birim sicim”i yarı yarıya küçüldüğünden aralarındaki mesafeyi 200A olarak ölçecektir. Küçülme işlemi zaman içinde gerçekleşirse gözlemci cisimlerin küçüldüğünü değil birbirlerinden uzaklaştıklarını düşünecektir. Çünkü gözlemci ve tüm ölçüm sistemleri cisimle orantılı olarak küçülmektedir. Bugün evrende aynen bu durumu yaşıyor olabiliriz. Kullandığımız “birim sicim” olan hafif sicim zaman içinde küçülüyorsa biz galaksilerin küçüldüğünü değil aralarının açıldığını düşünürüz. Bizim evren bakışımız fotonlar sayesinde olmaktadır. Bu demektir ki Sayın Greene’in dediği gibi fotonlar bizim “birim sicim” dediğimiz şeylerdir ve zaman içinde küçülmektedir.
Dediğimiz gibi evren bu durumdaysa o zaman sicim teorisinin mesafe tanımı için sunduğu “birim sicim”ler için her hâlükârda bir sorun görülmemektedir. Yani ister ağır sicimi ister hafif sicimi alalım evren her halükârda büzüşmelidir. İşte sicim teorisinin muazzam bir öngörüsü. Ayrıca bu durum, evrenin kapalı olması durumunda bile neden yeterli madde göremediğimizi de açıklar. Çünkü evren kapalı başladığı serüvenine günümüze gelene kadar kütle kaybettiği için artık yeterli madde kalmadığı gözükmektedir. Bu durumda evren açık duruma geçmiş olsa bile evrenin ölümü buharlaşma şeklinde olacaktır.
Evreni anlamak için kullandığımız hafif sicimin foton olduğunu biliyoruz. İşte bu fotonun zaman içinde büyüklüğünün değiştiğini söyledik. Bizim ölçü sistemleri dahil her şeyimiz bu fotonlar gibi küçülmektedir. Daha doğrusu büzüşmek tanımı sanki daha doğru gibi… Onun için ne zaman ölçersek ölçelim herhangi bir büyüklük aynı olacaktır.
“Evren kütle kaybediyor” savı ciddi bir iddiadır. Bilimin bugüne kadar, bu yönde bir araştırma yaptığını hiç duymadım. Eğer yaparlarsa ciddi deliller bulacaklardır. Evrenin kütle kaybediyor savının en ciddi delili bütün galaksilerin birbirlerinden uzaklaştıkları gerçeğidir. Bunu karanlık enerjiyle açıklama uğraşısı var ama şimdiye kadar hiçbir veri bulunamadı. Karanlık madde de dolaylı uzaktan bir delil oluşturabilir. Çünkü kütle kaybetmenin yolu Büyük Patlamada oluşan sürecin tersine işleyerek parçacıkların, görünen evrenden çıkmalarıdır. Bunun ilk aşaması karanlık maddedir. Yani kütleler bir şekilde evrim geçirerek karanlık maddeye dönüşmektedir. Eğer bu süreç Büyük Patlamanın tersiyse, maddeler bir şekilde dalga frekanslarını yükselterek enerji kazanmak zorundadır. Bunun nedenini henüz açıklayamıyoruz ama bu süreci yaşayan bir atomun, bir müddet sonra görüş alanımızdan çıkacağı kesindir. Görüş alanımızdan çıkmış olsa bile bizim boyutumuzu terk etmediği için kütle çekim etkisini hissetmeye devam ederiz. Fakat bu süreç devam ederse bir müddet sonra boyutumuzu terk eder. İşte o zaman artık kütle çekim etkisini hissetmeyiz böylece evren kütle kaybetmiş olur. Bu süreci yaşayan parçacıklar süper simetrik parçacıklar diye adlandırdığımız ama henüz elde edemediğimiz parçacıklar olabilir. Hatta bazı bilim insanları karanlık maddeyi bu parçacıkların oluşturabileceği savını dillendirmektedir. Fakat bilim onları parçacık hızlandırıcılarda arıyor. Oysa parçacık hızlandırıcılarda kullanılan her parçacık astral düzey elemanı olduğu için onları bu yöntemle asla bulamazlar. Maddenin dalga frekansını baz alan yeni bir yöntem gerekir.
Bu duruma bir veri de çubuklu sarmal galaksilerin garip yapıları olabilir. Fakat o konuyu daha sonra inceleyeceğiz. Bunlar haricinde kütle eksilmesinin başka verileri de olması gerekir. Gökyüzünü inceleyen teleskoplarımız sayesinde bir veriye daha ulaşıyoruz. Bu veri, süper kümelerin hatta büyük duvar gibi çok büyük oluşumların varlığıdır. Eğer evrende birbirine bağlı olmayan galaksiler bir küme oluşturabiliyorsa bunun sebebi kütle çekimin azalması olabilir. Öyle ya! Eğer bu galaksiler birbirlerinden artan bir süratle uzaklaşıyorsa birbirlerinden kopmuş olmaları gerekir. O zaman onlar küme oluşturamazlar. Eğer hem birbirlerinden uzaklaşıp hem de küme oluşturabiliyorlarsa bunun tek açıklaması kütle çekimin azalmasıdır. Şekil 7’deki durumun yaşandığını anlamalıyız. Aslında onlar gerçekten bir kümeler ve birbirlerinden uzaklaşmıyorlar aksine aralarındaki mesafe azalsa bile biz “birim sicim” nedeniyle aralarındaki mesafenin arttığını ölçüyoruz.
Bu durumda, hafif sicim olan fotonun, zaman içinde küçülmeye devam ettiğini söylemiştik ama bu küçülmenin ışık hızına da yansıması oluyordur. Yani ışık hızı da evrenin başlangıcından beri azalıyor olmalıdır.
Karadelikler, Paralel Evrenler olabilir mi?
Sicim kuramını doğru kabul ettiğimiz için, onun ön görüsü olan evrenin de, dairesel olduğunu kabul etmiştik. Hani sicim kuramının “birim sicim” ölçümünden evrenin dairesel boyutlardan oluştuğunu görmüştük. Bu durumun tüm boyutlar için geçerli olduğunu söylüyordu. Eğer evrenin dairesel olduğunu gösterebilirsek bu durum çok ciddi bir delile kavuşur. Hatta biraz hayalperestlik yaparak evrenin ilk değil, tali evrenlerden biri olduğunu da kabul edelim.
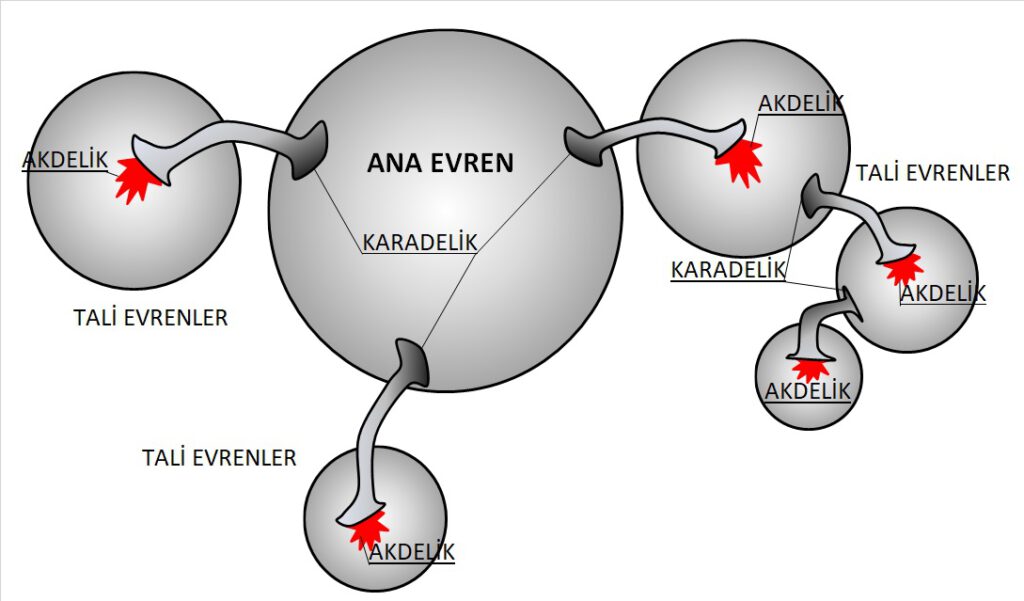
Şekil 8 İlk ana evren ve tali evrenler
Tali evren olarak şekil 8’deki yapıyı kastediyoruz. İlk olarak Büyük Patlamada çok fazla madde oluşacağı için çok büyük yıldızlar ve galaksiler oluşacaktır. Böylece çok fazla karadelik olacaktır. Orada oluşan her karadelik çok fazla madde yutacaktır. İşte, biz de öyle bir karadeliğin içindeki evren olabiliriz. Hatta belki de ikinci tali evrendeki bir karadeliğin içindeki evren bile olma ihtimalimiz vardır. Her tali evren şartlarını ilk oluşan evrenden alacağı için bütün tali evrenler aynı fiziksel ve kimyasal kanunlara tabi olacaktır. Çünkü karadelikler bilgiyi aktarmaktadır. Ayrıca her karadelik yuttuğu maddeyi ilk yapı taşı olan sicimlere kadar ayrıştırıp arkadan püskürttüğü için ilk Büyük Patlama şartları, her karadelik içinde geçerli olmuş olur. Böylece her karadelik bir paralel evren demektir. Paralel evren derken, görünen evrenin paralellerinden bahsediyoruz. Yoksa kuantum evrenin sadece ikizi vardır. Onun paralelleri olmaz.
Bütün paralel evrenler, insan gibi kompleks bir canlı üretebilir mi?
Paralel evrenler, genel olasılık dalgasının farklı çökme durumlarına denk gelir. Genel bir olasılık dalgası, her bir parçacığın bulunması muhtemel olan konumlarına işaret eden birçok sivri yapıya sahip dalgaların birleşimidir. Durumu daha iyi anlayabilmek için, şekil 9a’da dalgalı yüzey, olasılık dalgasıdır. Olasılık dalgasının yüzeyi onu oluşturan dikey çizgilerin tepelerindeki plâtodan oluşur. Şekil 9 c deki olasılık dalgası tek bir parçacığa ait dalgadır ve çöktüğünde en büyük olasılıkla en yüksek noktasına çökmesini bekleriz. (İlle Şekil 9 b deki gibi en yüksek tepeye çökmez ama olasılık olarak en güçlü olasılıktır). İşte astral düzey bütün parçacıkların olasılık dalgalarının toplamından oluşur. Şekildeki plato onların toplamıdır.

Şekil 9 Olasılık dalgası durumları
Sayın Greene, Schrödinger’in kuantum denkleminden görünen evrenin oluşumunu anlatabilmek için, şu örneği kullanmıştı. Sahnede dans eden bir dans topluluğunun bütün elemanları bir sahne gösterisi sırasında aynı anda yere çömelirken, içlerinden birinin yanlışlıkla çömelmeyi unutup ayakta kalması gibi, bir durum yaşanmaktadır. Schrödinger’in kuantum denkleminde çöken kısım (yani çökmeyi unutan dansçı) görülen evreni oluşturur. Bizim evrenimizde çöken oyunculardan biri, paralel evrenlerden birinde ayakta kalan kişi olacaktır. Böylece her paralel evrende başka bir dansçı çökmemiş olacaktır ama bu dansçıların hepsi aynı gurubun elemanlarıdır. Yani tek bir denklemin çeşitli görünümleri olacaklardır. İşte “paralel evrenlerde eşizlerimiz var olmalıdır” düşüncesi bu durumdan beslenir. (Brian Greene Saklı Gerçeklik)
Bu duruma göre her paralel evren insan gibi bir yapı üretmesi potansiyeli vardır ama eğer bir karadelik yeteri kadar madde yutmamışsa, arkasında oluşan evrende de canlı oluşabilecek kadar madde olamaz. Fakat bizim görünen evrenin tüm kanun ve kurallarına tabi olur.
Her maddenin olasılık dalgasının çökmemiş hali astral düzeydedir. Çökmüş hali görünen evrendedir. Bir yıldızın kendi içine çökerek bir karadelik oluşturması bir evrendeki maddelerin bir kısmını alarak yeni bir evren oluşturmasıdır. O maddelere karşılık gelen çökmemiş hal astral düzeyde varlığını sürdürmeye devam eder. Yani Daha önce de dediğimiz gibi her paralel evren, girdi şartlarını astral düzeyden alır.
Sicim kuramı için kozmik delil bulunabilir mi?
2010 yılında Physics Review B dergisinde çıkan, karadeliklerin zıttı varsayılan, “maddeyi yutmak yerine kusan akdelikler!” “Karadelik ve akdeliği birbirine bağlayan Einstein-Rosen köprüleri!” gibi kavramların sıkça kullanıldığı bir makalede evrenimizin başka bir evrende bulunan bir karadeliğin içinde olduğundan bahsediliyor. Poplawski, her karadeliğin genel görelilikte bir Einstein-Rosen çözümü olduğunu söylüyor. Karadelik oluşurken, eşzamanlı olarak, Einstein-Rosen köprüsünün diğer ucunda bulunan akdelikten başka bir evrenin oluştuğu öngörülüyor. Poplawski, bu evren modeli ile kozmolojideki bazı problemlerin -örneğin karadeliklerdeki bilgi kaybının- ortadan kalktığını belirtiyor. Bilim ve Teknik Mayıs 2010 Yeni bir Evren Modeli Zeynep Ünalan
Poplawski’nin iddiasını ciddiye alıyor ve bir üst evrendeki karadeliğin içindeki evrende yaşadığımızı iddia ediyorum. O zaman şekil 8’deki tali evrenlerden birinin içindeyiz. Aslında ikincil bir evrende olduğumuzu anlamanın bir yolu var. Eğer ikincil bir evrendeysek, evrenimizde bir tane beyaz delik olmalı. Bizim yapmamız gereken şey, beyaz delikleri tanımlayıp evrenimizde olup olmadığını bulmak.
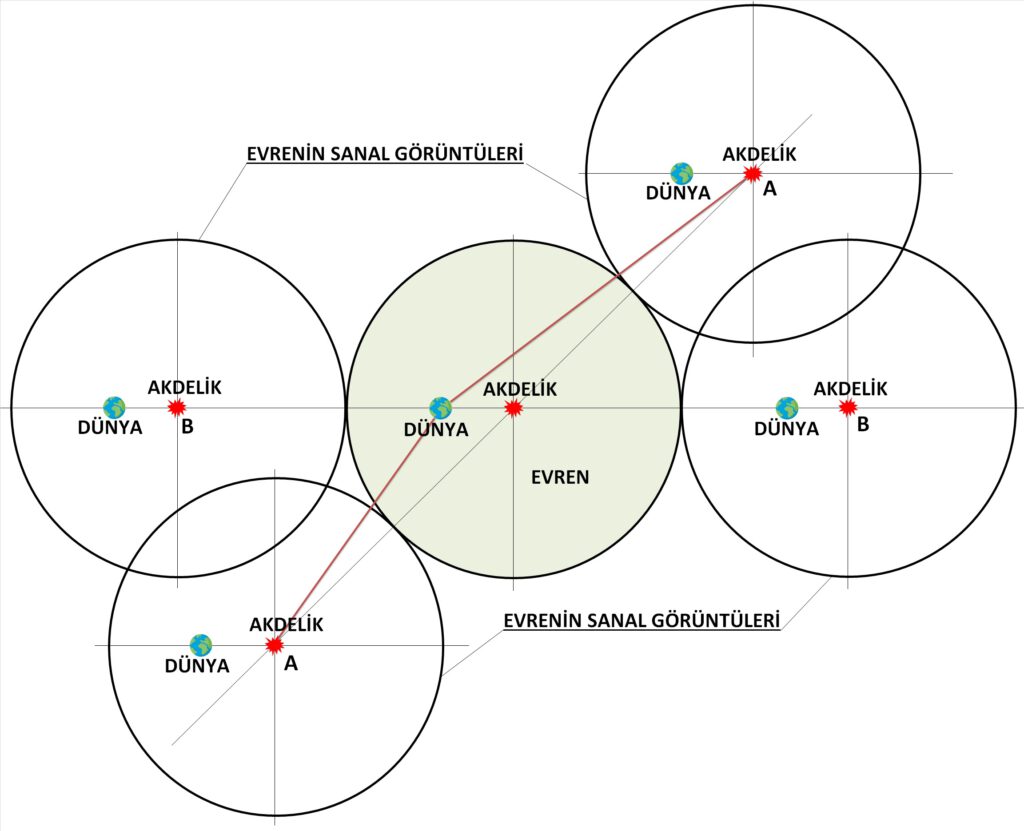
Şekil 10 Aynı akdeliğin farklı görüntüleri
Beyaz deliği tanımlamak gerekirse öncelikle evrene muazzam ölçülerde madde püskürtmeli ve bir karadelik ölçülerinde olmalı. Birde çok uzun zaman önce faaliyette olmalı. Günümüzde tamamen sessiz olma ihtimali yüksek olabilir. Elbette bunu kesin olarak bilemeyiz ama yakınlarda samanyolu galaksisinin merkezindeki karadeliğin görüntüleri yayınlandı, oradaki karadelik oldukça sessizdi. Madde yutmadığı için öte tarafa da madde püskürtemez. Evrenimizde böyle sessiz bir karadeliğin arkasında olması muhtemeldir. Fakat her halükârda zaman içinde madde yutmuştur. Beyaz delik, püskürttüğü madde her yöne dağılacağı için evrenin merkezinde olması gerekir. Uzayda bir delik tam bir küre olduğu için tüm yönlere madde püskürtebilir.
Evrende bu tanımlara uyan pek çok kuasar denilen gök cismi var. Kuasar, aşırı parlaklığa ve kütleye sahip gök cismidir. Yaydığı enerji ve ışık miktarı o kadar büyüktür ki, bu miktarda bir enerji, bir galaksideki tüm yıldızların yaydığı enerjiden daha fazla olabilir. Demek ki aradığımız şey kuasar olabilir ama şöyle bir sorun var, bir değil yüzlerce kuasar tespit edildi.
İşte aradığımız cevapta burada olabilir. Eğer evren dairesel (yani hiper küre ya da hipertorus) ise bizim tek bir kuasarı pek çok yerde görmemiz gayet mantıklıdır. Zaten gördüğümüz hemen bütün kuasarlar evrenin uçlarında. Yani beklediğimiz gibi. Fakat evrenin tam merkezinde de bir tane görebilmeliyiz ama, onu görebilmemizin yolu, bize ulaşan fotonların yola çıktığında kuasarın faaliyette olmasına bağlı. Faal değilse onu göremeyiz. Şekil 10’da evrenin merkezinde bir akdelik olması durumunda o akdeliği göreceğimiz birkaç pozisyon görülmektedir. Ortadaki küre içinde bulunduğumuz evren ise etraftaki küreler, evrenin sanal görüntüsü olacaktır. Eğer akdelik ile dünya evrenin çapı üzerindeyse 180 derece açıyla ters yöne baktığımızda da ( yani B-B aksı) aynı kuasarı görebilmeliyiz. Yok çap üzerinde değilsek (yani A-A aksı) o zaman ters yöne baktığımızda göreceğimiz akdelik, tam 180 derece açı üzerinde olmayacaktır. Açının 180 dereceden sapma büyüklüğü, evrenin merkeziyle dünya arasındaki uzaklığa bağlı olacaktır. Elde ettiğimiz evrenin uçlarındaki kuasarların aynı akdelik olduğunu kabul edip, şekildeki mantığı baz alarak, üç boyutlu haritaya yerleştirmemiz durumunda, evrenin yapısı ortaya çıkacaktır. En azından evren hakkında önemli bilgilere ulaşırız. Elbette uzağa bakmak, aynı zamanda geçmişe bakmak olduğunu bilerek gözlemleri değerlendirmek gerekir.
Evrenin büyüklüğünü başka bir yöntem ile de anlayabiliriz. Büyük kütlelerin ayna etkisi sebebiyle arkalarında kalan cisimlerin birden fazla görüntüsünü oluşturduğunu biliyoruz. Benzer etki tam tersten bakınca da olabilir. Bu epey şanslı bir durum gerektiriyor olsa da dikkate almaya değer bir yöntem. Kısacası astronomlar evrenin çok büyük olmadığını düşünürse mutlaka dâhiyane çözümler bulacaklardır.
Evrenin hiper küre olması onun aynı zamanda dışının olamayacağını gösterir. Evrende sonsuza kadar bir yöne yolculuk yapsak bile evrenin dışına çıkamayız. Aynı galaksilerin yanından geçip dururuz.
Evrendeki boşluk veya madde yığınları nasıl oluştu?
Evrenin oluşumunu anlatırken, ilk oluşan sicimlerin bazılarının, antilerini bularak yok olduklarını söylemiştik. O olayı detaylandırırsak, her patlama merkezi dışa doğru bir itki oluşturacağı için sicimlerin patladığı yerler boş kalacaktır. Şekil 11’de görüldüğü gibi patlama merkezlerinden uzaklaşan maddeler, ara boşluklara yığılmak zorunda kalmıştır. Elbette evrendeki sicim patlamaları bu kadar düzenli olmamıştır. Daha çarpık bir yapı vardır. Çünkü bazı noktalarda birkaç sicimin beraber patlamış olabileceğini de düşünmek mantıklıdır. O durumlarda oluşan boşluk devasa olacaktır. Çoban boşluğu bu tür bir boşluk olabilir. Büyük duvar diye adlandırılan yapı da şekil 11’dekine benzer bir yapı olabilir. Şekilde görülen banyo suyundaki sabun köpüğü de kabarcıkların boşluğu doldurma uğraşısıdır. Orada büyük baloncukları sicim antisicim patlama merkezi olarak kabul edersek küçük baloncuklar maddeye karşılık gelir ve gördüğünüz gibi aralara sıkışmışlardır. Evrendeki madde büyük baloncukların aralarında kalan yerlerde toplanacağı için örümcek ağı ya da beyin nöronları şeklinde bir yapı oluşacaktır. Evrenin kozmik tarihi içinde, bazı galaksiler kütle çekim sebebiyle boşlukların içine doğru savrulmuş olabilir. Fakat genel yapı böyle olmalıdır.
Evrenin eş ve zıt yapısı
Buraya kadar anlattığımız evren yapısını tek bir çatı altında topladığımızda şekil 12’deki evren yapısına ulaşırız.
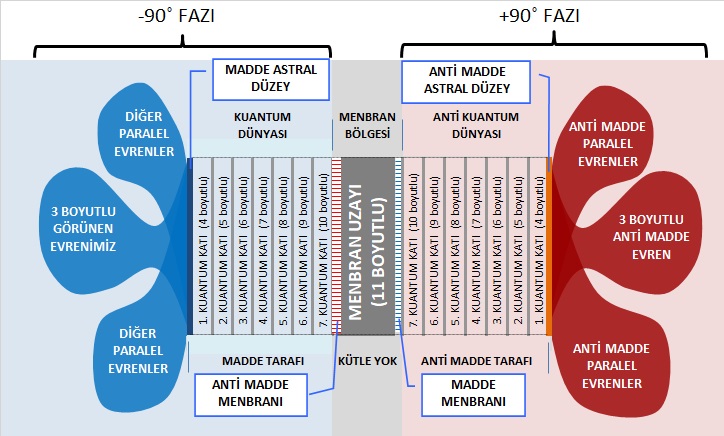
Şekil 12 Eş ve zıt evren yapısı
- M kuramının tanımladığı menbranların olduğu 11 mekân boyutlu bölge şeklin ortasındaki bölgedir.
- Bu bölgede bulunan iki zıt menbran birbiriyle çarpıştığında oluşan parçacıkları zıt menbranlar çektiği için her menbranın olduğu yerde karşı menbrandan oluşan parçacıkların kuantum evreni oluşur.
- 10 boyutlu uzayda oluşan sicimlerin enerji kaybetmeleri sonucu 7 kuantum katını aşan madde astral düzey denen iki karşı fazda toplanır.
- Oluşan ilk iki zıt ana evrendeki maddelerin karadelik oluşturmaları sonucu her iki fazda da muazzam sayıda karadelik oluşacaktır. Oluşan her karadelik bir alt evren oluşturacaktır. Fakat yanlış anlaşılmaması açısından ilk ana evren de bu evrenlerle aynıdır. Yani oda tam bir paralel evren yapısındadır.
- Biz bu alt evrenlerden birinin içindeyiz. Şekildeki mavi “3 boyutlu görünen evrenimiz” ile gösterilen balon, bizim evrenimizdir ve karşı fazda da ikiz paralel evrenimiz vardır. Bizim gibi her paralel evrenin bir ikizi vardır. Bu durum, Schrödinger’in kuantum denkleminin bir de karşı denkleminin olması gerektiğini söyler.
- İkiz paralel evrende bizim ikizimiz olabileceği gibi bizim paralel evrenlerde de bize çok yakın frekansta eşizlerimiz olacaktır. Zaten daha önce Schrödinger’in kuantum denkleminden evrenimizin oluşumunu anlatabilmek için kullandığı örnekte her paralel evrende çökmeyen dansçının bizim eşizimiz olabileceğini söylemiştik. İşte bizim eşizlerimiz şekildeki mavi renki baloncuklardadır. İkizimizin eşizleri de kırmızı renkli baloncuklardadır.
- Her paralel evren veya ana evren tüm girdilerini astral düzeyden alır. Onun için hepsinin kanun ve kuralları aynıdır ama, hepsinde insan türü canlı oluşup oluşamayacağı konusu tartışılır. Örneğin, ilk ana evrende çok fazla madde olacağı için çok büyük yıldızlar olacağını söylemiştik. Çok büyük yıldızlar, çok kısa sürede kendi içine çökerek karadeliğe dönüşecektir. Bu da orada çok fazla kaos olacağını gösterir. Bu durumda, dünya benzeri yapıların oluşması için, hem gereken zaman olmayabilir hem de çok fazla kaos canlı oluşumuna engel olabilir. Onun için, insan türü canlı oluşamayacağı düşünülebilir. Aynı durum yeterli madde yutamayan karadelikler için de geçerlidir. Yeterli miktarda madde yoksa, insan da oluşamaz.
- Eğer paralel evrenlerdeki bir atom, bir şekilde enerjisini artırıp alt parçacıklarına ayrışırsa, enerji seviyesi arttığı için frekansının da artması gerekeceğinden, oluşan parçacıklar, şekildeki astral düzeyin üzerine çıkacaktır. Böylece bizim görüş alanımızın dışına çıkar ama hâlâ kütle çekimsel etkisini hissetmeye devam ederiz. Kütle çekimsel etkiden çıkabilmesi için ikinci kuantum katına geçmesi gerekir.
Maddenin yapı taşları olan sicimlerin yapısı nasıldır?
Bu konuya çok farklı bir bakış açısıyla bakalım. Büyük kütlelerin kendi içine çökerek karadeliğe dönüşmelerini düşünelim. Yani tüm madde çöküp tek noktada bir karadeliğe dönüşüyorsa, acaba bunun nedeni aslında maddenin temel yapı taşının da bir mini karadelik olmuş olması olabilir mi? Yani eğer, sicimlerin yapısı bir mini karadelik ise, madde çöktüğünde sicimler birleşerek kocaman çekim gücü olan bir kara deliğe dönüşmesi beklenebilir.
Zaten, Stephen Hawking’de evrenin ilk oluşum anlarında mini karadeliklerin yani Kuantum mekâniksel Karadeliklerin, olması gerektiğini söylemişti. Acaba bu söylediği karadelikler, sicimler olabilir mi? Gerçi o mini karadeliklerin buharlaşmış olması gerektiğini de söylemişti. Fakat buharlaşma için kurduğu mantık, ya hatalı ya da benim anlayamadığım başka bir durum var.
Hawking ışıması olarak adlandırılan süreç, boş uzaydaki kuantum dalgalanmaları sonucunda madde – anti madde çiftlerinin oluşmasıyla başlar. Bazen olay ufkunun yakınında oluşan parçacıklardan biri, karadelikten uzaklaşırken diğeriyse karadeliğin içine düşer. Bu süreç sonunda karadeliğin dışında kalan parçacık pozitif enerjiye sahip olduğu için karadeliğin enerjisi ve dolayısıyla kütlesi azalır. Fakat burada anti parçacığın karadeliğe düşmesi için seçici bir faktör olması gerekir. Oysa yukarıda kütle çekimini anlatırken bu durumun tersini anlatmıştık. Yani kütle çekim maddeyi çeker, anti maddeyi iter. Böylece karadeliğe düşmesi gereken anti madde parçacık olmayacaktır. O da uzayda çarpışacağı bir madde parçacığıyla yok olacaktır. Böylece karadelik yok olmak yerine, büyüme eğiliminde olacaktır. Evren kütle kaybederken karadeliğin kütlesi artacaktır. Toplam denge korunacaktır.
Fakat Hawking’in bulduğu buharlaşmanın mekanizması söylediğimiz gibi madde eksilmesi yüzünden ise bu Hawking’in muazzam bir öngörüsü demektir. Doğal olarak o, bu sürecin tüm eş ve zıt evreni kapsadığını anlayamamış olabilir. Çünkü hiçbir kuramımız ve gözlemimiz, evrenden madde eksildiğini direk söylemediği için, “düşünmüş olsa bile” çok uçuk gelmiş olmalıdır.
Konumuza dönersek, eğer sicimler bir karadelik ise yapılarının dört tür olması gerekir. Karadelikleri inceleyen bilim insanları onların dört çeşit olduklarını hesapladılar.
1- Açısal momentum ve elektriksel yük sıfır değerliyse “Schwarzschild karadeliği” türü söz konusudur.
2- Karadeliğin elektriksel yükü sıfır olmayıp açısal momentumu yani kendi ekseni etrafında dönüşü sıfır olduğu takdirde “Reissner-Nordström karadeliği” türü söz konusu olur.
3- Karadeliğin bir açısal momentumu olup elektriksel yükü olmadığı takdirde “Kerr karadeliği” türü söz konusu olur.
4- Kerr karadeliğinin elektriksel yüke sahip olduğu türdür. Buna Kerr-Newman karadeliği türü denir.
Bu yapı mini karadeliklerin de yapısının aynısı olacaktır. O zaman evrende bulunan yüklü ve yüksüz her parçacığın kökeni bu karadeliklere dayanması gerekir. Yani sicimler, hadronlar ya da leptonlar bu mini karadeliklerden oluşmalıdır. Tahmini bir eşleştirme yapalım.
- eelectron (Elektrik yükü=-1) ………Reissner-Nordström karadeliği.
- νenötrinolar (Elektrik yükü=0) .……Schwarzschild karadeliği.
- kuarklar (çeşitli yüklerde)…….…..…Kerr-Newman karadeliği.
- Bozonlar(Elektrik yükü=0) …………Kerr karadeliği.
Bu eşleştirmeye göre yüklü karadelikler kütleyi, yüksüz karadeliklerse kütleler arasındaki ilişkiyi düzenler. Böylece evrende var olan her şey bu dört mini karadeliğin eseri olmuş olur. Evrendeki büyük kütleli karadelikler maddenin de yapı taşı olan Kerr-Newman karadeliği olmalıdır. Yani hem açısal momentumu hem de elektriksel yükü olmalıdır. Burada bahsedilen elektriksel yük, kütle çekimi oluşturan ve anti menbranla maddenin birbirini çekmesini sağlayan yük olduğunu belirtmekte fayda var. Fakat bu bildiğimiz elektriksel yüklerle etkileşmeyen başka türlü bir elektriksel yük olmalıdır. Onun için kütle çekim formülleri elektriksel yüklerin formülleriyle aynıdır.
Bu duruma göre de dört adet sicim teorisi olması gerekirdi. Beş adet teorinin ne anlama geldiğini anlayamıyorum.
Kuantum mekaniğinin gariplikleri anlaşılabilir mi?
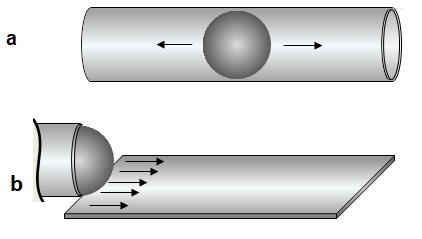
Şekil 13 Tek boyuttan iki boyuta geçen top hangi doğrultuyu seçer?
Önce belirsizlik ilkesini inceleyelim. Durumun daha kolay anlaşılabilmesi için şöyle bir örnekleme yapalım. Evrenin, şekil 13 a’daki gibi bir hortum evren olduğunu düşünelim. Hortumun içindeki bir bilyenin hareketine bakalım. Hortumun içinde bilyenin hareket edebileceği yön olarak ileri veya geri hareket olacaktır. Eğer biz hortumu, boyunca kesip bir yüzeye çevirirsek, bu sefer bilye yüzey üzerinde iki boyut boyunca karmaşık hareketler yapabilecektir. Düz hareket yapsa bile şekil 13b’deki oklardan hangisini seçecektir. Yüzey üzerinde pek çok doğrultu seçilebilir. Bu durumu üç boyuta yükselttiğimizde tek boyuta karşılık gelen sonsuz yer var demektir. İşte işin püf noktası burasıdır. Bilye bir yeri tercih edemez. Bilye hortum içindeyken çapı oluşturan çember boyunca her noktası hortuma temas ederken hortumu kesip açtığımızda yüzeye tek noktadan temas edecektir. Aslında iki boyutlu yüzeyin her noktası onun için aynı değerdedir. Elbette bir yeri tercih edemez ama olması gereken yer konusunda da çok serbest değildir. Olması gereken bir bölge vardır. Örneğimizdeki bilye, iki boyutlu yüzeyin dışına çıkamaz. Kaba bir benzetme olmasına rağmen belirsizlik ilkesinin nedeni ve mantığı budur. Parçacığın boyutu artmazken mekânın boyutunun artmasının getirdiği belirsizlik…
Bu duruma yine “birim sicim” açısından bakmamızı gösteren bir durum. Eğer olaya ağır sicim açısından bakarsak evrenin çok çok küçük (Planck sabitinin 1061’de biri) olduğunu anladığımızda sicimlerin tercih etmeleri gereken bir yer olmadığını bunun sadece hafif sicimi tercih ettiğimizde karşımıza çıkan bir durum olduğunu anlıyoruz. Şekil 13a’da hortum içindeki bir bilye olarak düşündüğümüz şey ile şekil 1’deki evren yapısındaki sarılı sicim aynı şeydir. Evrenin de kesilip açılamayacağını söylemeye gerek yok. Biz hafif sicim ile evrene baktığımız için, evren içinde gezebiliyoruz gibi bir durum doğuyor. Baktığımız bu açı kuantum evren için geçerli olmadığı için garipliklerle karşılaşıyoruz. Kısacası evrene doğru bakış açısı ağır sicimdir. Ağır sicimle bakabilsek bu gariplikler olmaz.
Dolanıklık konusunu da bu gözle değerlendirmek gerekir. Dolanıklığı; iki eş parçacığın birbirlerinden milyonlarca ışık yılı uzakta olsa bile parçacıklardan birine yapılan etki diğerini anında etkiler” olarak tanımlıyoruz. İşte bizim olaya ağır sicim açısından bakmamız gerektiğine işaret eden başka bir durum. Eğer ağır sicim açısından olaya bakarsak evrenin çapının Planck mesafesinin 1061 de biri olduğunu söylemiştik. Yani aslında uzak diye bir kavram yok. Bu sadece bizim olayı farklı değerlendirmemizden başka bir şey değil. Evren için ağır ya da hafif sicim ayrımı yoktur. O zaman bu parçacıkların birbirinden ayrı olduklarını görmemiz bir yanılsamadır. Eğer dikkat ederseniz en büyük sorun hız ve mesafe kavramlarında vardır. Bu da kuantum evrende mesafenin olmadığı anlamına gelir. Mesafe olmayınca hız kavramı da anlamsızlaşır.
Çubuklu sarmaL galaksilerdeki garip durum.
Çubuklu sarmal galaksilerin kütle çekim kurallarına uymadıkları bilinir. Merkezlerinde oluşan çubuk bölgesi kütleçekim kurallarını alt üst eder. Şekil 14b’deki NCG 1300 galaksisinden, durum anlaşılabilir. Üstelik merkezdeki çubuk oluşumu kozmik tarihin ikinci yarısında başlamış.

Şekil 14 Güneş ve gezegenlerinin konum/hız grafiği, çubuklu sarmal galaksideki konum hız grafiğiyle aynı
Bizim teorimiz açısından bu çubuğun oluşum hikayesi önemlidir. Çünkü bu hikâye teorimizi destekleyen bir yapıdır. Öncelikle durumun tespitini yapmak gerekir.
Şekil 14’de güneş sistemiyle çubuklu sarmal galaksi arasındaki benzerliği görebilirsiniz. Güneşin içindeki atomlar dahil çevresindeki gezegenlerin merkeze uzaklık/hız grafiğini görmekteyiz. Aynı durum çubuklu sarmal galaksi içinde geçerlidir. Güneş sistemi için garip bir durum yok ama sarmal galaksinin çubuk bölgesi için ciddi sorun var. Çubuk bölgesi beklentiler gibi bir grafik oluşturmamış. Grafiğe göre galaksinin çubuk bölgesiyle güneş gövdesi içindeki atomlar aynı davranmış. Güneş içindeki atomlar birbirlerine bağlandığı ya da bağımsız hareket edemediği için bu tür bir grafik çizmeleri normaldir ama galaksideki serbest yıldızlar için aynı durum söz konusu değildir.
Galakside çubuk bölgesini oluşturan yıldızların tümünün açısal hızlarını aynı yapan sebebi bulabilmek için karanlık maddeden yararlanacağız. Eğer evren görünen maddenin 5 katı karanlık madde içeriyorsa o zaman aynı durum bu galaksi için de geçerlidir. Galaksilerdeki karanlık maddeler her sistemde olduğu gibi kütle çekim nedeniyle merkezde toplanmak durumundadır. Bu da şöyle bir seyir izlemelidir. Başlarda karanlık madde oluşurken galaksinin ortalama dönüş hızını taklit edecektir. Çünkü görünen madde kendi dönüşünü kütle çekim sayesinde ona aktaracaktır. Karanlık madde büyüdükçe çubuk uçlarındaki yıldızları tutarak kendi hızına senkronize edecektir. Karanlık maddenin çapının içine giren her yıldız artık karanlık madde küresinin bir elemanı olacaktır. Elbette karanlık madde küresi ilk başta karadeliğin dönüş hızıyla özdeş olacaktır. Fakat kürenin çapı arttıkça momentumun korunumu sebebiyle dönüş hızı yavaşlayacak ve yüzey hep yörünge hızına denk gelecek hızda olacaktır. Karanlık maddenin dönüş hızı yavaşlarken merkeze yakın yıldızlar bu yavaşlamaya uyum gösteremeyebilir. Fakat yeterli süre geçtiğinde karanlık madde kütleçekim kuvveti nedeniyle onları da kendisine bağlayacaktır.
Peki neden çubuk bölgesi, zaman içinde uzar? Eğer savımız doğruysa, kesinlikle merkezdeki karanlık madde zaman içinde artıyor demektir. Tıpkı güneş sisteminin ilk oluşum anında çevresindeki maddeleri kendine çekip yavaş yavaş büyümesine benzer bir durum. Karanlık maddeler bir şekilde artıp merkezdeki hayali kütleyi büyüttükçe, o da en yakın yörüngedeki yıldızları tutmağa ve çubuğa eklemeye başlıyor. Daha doğru anlatımla merkezdeki görünmeyen kütle en yakındaki yıldızın yörüngesini kapsayacak şekilde büyüdüğünde hem o yıldızı tutuyor hem de kütle olarak büyüdüğünde kendi ekseni etrafındaki hareketi yavaşlayıp son tutulan yıldızın yörünge hızına düşüyor. Böylece, büyüdükçe; görünen yıldızlar, hep çubuğun ucuna eklenmiş oluyor. Bir kütlenin çapı büyüdükçe momentumun korunumu sebebiyle dönüş hızının yavaşlaması bilinen bir durumdur.
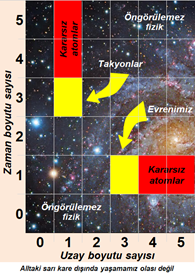
Şekil 15 Alttaki sarı bölge dışında yaşamamız pek mümkün değil (Bilim Teknik Ağustos 2004)
Fakat şöyle bir sorun olmalı. Bildiğimiz büyük kütleler kendi çekim güçleri altında çökmeye mahkûmdur. Üstelik çubuk bölgesini oluşturan karanlık madde küresinin çapı binlerle tanımlanabilecek ışık yılı mesafe olacaktır. Yani evrende o büyüklüklere yaklaşabilecek bir yıldız olamaz bile. Şöyle düşünün galaksinin yarısından daha büyük, tek bir yıldız olabilir mi? Olamaz, çünkü oluşurken çoktan kendi içine çökmesi ve çubuk bölgesinin bozulması gerekirdi.
Çökmenin olmamasını söyle açıklayabiliriz. Amerika, New Jersey’deki İleri Çalışmalar Enstitüsü’nden araştırmacı Max Tegmark, “evrenin uzay boyutu, üçten fazla olsaydı, yaşam mümkün olamazdı” diye söylemektedir. “Evren’in üçten fazla uzay boyutu olsaydı, ne Güneş’in etrafında gezegenler, ne de atom çekirdeği etrafında elektronlar yörüngede kalabilirdi.” (Science er Vie, Ocak1998) demektedir. Yani evrenin büyük kütleler oluşturabilmesi için 3 uzay boyutuna sahip olması gerekir. Eğer evren 4 uzay boyutuna sahip olsaydı Şekil 15’de gözüktüğü gibi güneş gibi büyük kütleler oluşamazdı. Hatta atom bile kararlı olamazdı. İşte çubuklu sarmal galaksilerin merkezinde oluşan o büyük karanlık madde yıldızı 4 boyutlu uzayın içindedir. Böylece onu göremiyor oluşumuza karşın merkezde bir kütle varmış gibi davranmaktadır. Çünkü çekim gücünü, 3 uzay boyutlu evrenimizde hissedebiliyoruz. Aslında karanlık madde evrene eşit dağılma eğilimindedir ama görünen maddenin onu galaksi merkezinde toplaması söz konusudur. Böylece merkezde kocaman bir kütle olmasına rağmen bu kütle kendi içine çökemez. Onların bir arada durmasını sağlayan şey kendi çekimleri değil görünen maddedir. Böylece birbirini etkileyen görünen madde ve karanlık madde, tıpkı bir yıldız gibi davranarak çubuk bölgesini oluşturabilmektedir.
Bu durum teorimiz için de ciddi bir delil oluşturmaktadır. Karanlık maddeyi oluşturan parçacıkların atomdan evrilmiş proton, nötron ve elektron olduğunu kabul etmemiz mantıklı olacaktır. Zaten biz bu parçacıkları süpersimetrik parçacıklar olarak biliyoruz. Madde evrim geçirerek ilk aşamasını tamamlamış ve ikinci aşamaya doğru evrime devam etmektedir. İkinci aşama karanlık maddenin 4 mekân boyutlu uzaydan çıkarak kütleçekim etkisini artık hissetmediğimiz bir duruma dönüşmesidir. O zaman görünen evren kütle kaybetmiş olacaktır.
Şekil 5’deki yapıya bakarak küçük bir özet yapmak gerekirse; Görünen evren atom denen dış kabuğun dışını kapsamaktadır. Bu bölge 3 mekân 1 zaman boyutuna sahiptir. Şekilde ilk iki kabuk arasında kalan bölge 1. Kuantum katı yani 4 mekân 1 zaman boyutlu bölge. Atom denilen kabuk ise astral bölge… Bu bölge 3 ile 4 mekân arasındaki sınırdır. Atom buranın elemanıdır. Bu yapıya bakarak atomun hem 3 hem de 4 boyutlu özellikler sergilemesi gerektiğini söyleyebiliriz. Yani bakış açısı durumu belirler. Atom en küçük bir evrim geçirdiğinde, parçalanarak süpersimetrik parçacıklarına dönüşüp görüş alanımızdan çıkar. Bunu yapabilmesi için dalga frekansını artırması gerekir. Fakat bizler atomu parçalayabiliyoruz. Parçaladığımızda elde ettiğimiz elemanlar astral düzeyin elemanlarıdır. Onun için onlar bizim görüş alanımızdan çıkmazlar. Görüş alanımızdan çıkan elemanların dalga frekanslarının artması gerekir. Maddenin dalga frekansını yükselten mekanizmanın nasıl bir şey olduğunu şimdilik bilmiyoruz.
Bu teoriyle; Standart Model, Sicim teorisi, M kuramı, Kuantum Mekaniği, Paralel evrenler, Karadelikler Kuramı, Büyük Patlama, Kütle Çekim, Süper simetrik parçacıklar teorilerini birbirine bağlamış olduk. Hatta karanlık madde ile karanlık enerjinin ne olduğunu da anlayabildik.
Seyfullah Demir
[1] Astral kelimesi o düzeyi temsil edebilecek başka bir kelime olmadığından tercih edilmiştir.
[2] Çift yarık deneyi sonuçları bu durumu bize gösterir.
yaklaşık 8 yıl önce
anu anlatıyoru okudunuz mu
yaklaşık 8 yıl önce
Cin masallarını okumaya değer bulmuyorum… Sümer kayıtları deşifre olana kadar ortada mısır tanrı isimleriyle boy gösteriyorlardı. Çivi yazısı söküldükten, hele Sichcin den sonra ortalığı Sümer tanrıları celseleri doldurdu…
yaklaşık 8 yıl önce
Zıt evrende olan ikizimizin bizi çekmesi yüzünden yerçekimine uğruyoruz değil mi?biz eksi yük o artı yük olduğu için birbirimizi çekiyorsa etrafımızda bir artı yük oluşturalım isimler birbirlerini de uçalım ne dersiniz.etrafı artı olan kürenin içinde elektrik alan yoktur.benzer şekilde yerçekimi alanında olmasa gerek ne dersiniz.
yaklaşık 8 yıl önce
Bizi çeken şey zıt evren değil, karşımenbrandır. Yani bizim oluştuğumuz menbran değil diğer menbran karşı olduğu için bizi çeker. Bizim oluştuğumuz menbran da zıt evreni çeker. Evren ve antievren birbirini algılamaz. Kütle çekimsel olarak da birbirini algılamazlar. Biri sıfır derece fazındaysa diğeri 180 derece fazındadır… Birbirlerini algıladıkları an birleşip gama ışınına dönerler…
yaklaşık 8 yıl önce
hani tekbir ruhun görüntüsüyüz demiştik ya .astralden bir atom eksilince tüm paralel evrenlerden de eksilir demek tüm paralel evrenler tek bir ruhun görüntüsüdür. doğru mu anlamışım
yaklaşık 8 yıl önce
Dünya gezegeninde kalu bela ile kıyamet arasında tekamüle sokulan tüm ruhlar tek bir ruhtur. Bu ruh kaynağa dönüşünde bir atomu astralden eksiltir. Paralel evrenler de girdi bilgilerini astralden aldığı için onlarda da bir atom eksilir. Fakat onlardaki eksilme sadece girdilerde eksilme olduğu için olmuştur. Oysa dünyadaki eksilme gerçek eksilmedir.
Kısacası aynı durum paralel evrenlerde de yaşanır ama gerçek eksilme sadece tek bir evrende olur. Bunu şöyle düşünebiliriz. Bir su deposuna bin tane musluk bağlıdır. Bu musluklarda birini açıp bir miktar su akıtalım. Depo, astral düzey; açık musluk ise bizim evrenimiz olsun. Biz musluğu açtığımız için depodan bir miktar su eksildi. Diğer musluklarda depodaki suyun eksilmesinden etkileniyor ama eksilmenin sebebi değiller. Bir müddet sonra aynı musluğu açıp bir müddet daha akıtalım. Bu demektir ki astralden iki atom eksildi. İlk atom ile ikinci atom bile aynı görüntü değil. Sadece Kalu belada oluşturulan ruhun görüntüleri tek ruhtur. Bu ruhun görüntüleri pek çok paralel evrende bedenlense bile onlar tek bir ruhun görüntüleridir.
Bir evrende sayısız kalu bela oluşurturulabilir… Zaten evrendeki atom ve karanlık madde miktarına bakarsak muazzam sayıda paralel evren olması gerektiği ve defalarca tekamül sistemini tekrarlamış olması gerektiği ortaya çıkar.
Paralel evrenlerin hepsi bir programdır hemde birbirinin kopyalarıdır. Dünyada ruh olarak bedenlendiğimizde şu durum oluşur. Biz olasılık dalgasının en tepe noktası isek, hemen yanımızdakiler başka başka paralel evrenlerdedir. Bize çok benzerler ama biz değildirler. Olasılık dalgasında bizden uzaklaştıkça benzerliğimizde azalır. Ruh eşi dediğimiz olasılık dalgasında hemen yanımızda olanlardır. Ama dediğim gibi biz değildirler…